Triangle 2

Triangle:- A polygon with three edges, three vertices and three angles is called Triangles. A triangle with vertices A, B, and C is denoted by ∆ABC.

**********************************

Existence of a triangle

A Triangle Is Exist If

* If sum of lengths of any two sides side is greater than third side.

AB + BC > AC

BC + AC > AB

AB + AC > BC

A Triangle is not possible if sum of lengths of any two sides side is less than or equal to third side.

*1. If sum of lengths of any two sides side is less than to third side.

AB + BC < AC

BC + AC < AB

AB + AC < BC

*2. If sum of lengths of any two sides side is equal to third side.

AB + BC = AC

BC + AC = AB

AB + AC = BC

**********************************

A Triangle Is Exist If

* If each of the angles is positive.

* If the sum of the all three angles is Supplementary (180°).

∠A + ∠B + ∠C = 180°

* It is also known as Angle Sum Property Of A Triangle so that we can say it in short ASPOT.

* A Triangle is not possible if sum of all the three angles is less than or more than 180°.

*1 A Triangle is not possible if sum of all the three angles is less than 180°.

∠A + ∠B + ∠C < 180°

*2 A Triangle is not possible if sum of all the three angles is more than 180°.

∠A + ∠B + ∠C > 180°

**********************************

Special Names Of The Sides Of The Triangle.

Hypotenuse :- Side opposite to right angle is called Hypotenuse.

We also used this name for opposite side of a given angle.

Base :- Horizontal side of a triangle is known as base.

Base is the adjacent side of a given angle.

Perpendicular :- Non-horizontal side of a triangle is known as Perpendicular.

Perpendicular is the other adjacent side of a given angle.

Perimeter: The sum of the lengths of all the three sides of a triangle is called perimeter.

Perimeter = AB + BC + AC

**********************************

A triangle with vertices A, B, and C is denoted \triangle ABC. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane. Wikipedia

Area: ½ × base × height

Perimeter: sum of side lengths of the triangle

Number of vertices: 3

Number of edges: 3

Internal angle: 60° (for equilateral)

Sum of interior angles: 180°

Line of symmetry: 3

Triangle
A triangle
Edges and vertices	3
Schläfli symbol	{3} (for equilateral)
Area	various methods; see below
Internal angle (degrees)	60° (for equilateral)

Triangle = Tri (three) + Angle

In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted.

Types of triangle

Euler diagram of types of triangles, using the definition that isosceles triangles have at least 2 equal sides (i.e., equilateral triangles are isosceles).

The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification are either a direct transliteration of Euclid's Greek or their Latin translations.

By lengths of sides

Ancient Greek mathematician Euclid defined three types of triangle according to the lengths of their sides:^[2]^[3]

Greek: τῶν δὲ τριπλεύρων σχημάτων ἰσόπλευρον μὲν τρίγωνόν ἐστι τὸ τὰς τρεῖς ἴσας ἔχον πλευράς, ἰσοσκελὲς δὲ τὸ τὰς δύο μόνας ἴσας ἔχον πλευράς, σκαληνὸν δὲ τὸ τὰς τρεῖς ἀνίσους ἔχον πλευράς, lit. 'Of trilateral figures, an isopleuron [equilateral] triangle is that which has its three sides equal, an isosceles that which has two of its sides alone equal, and a scalene that which has its three sides unequal.'^[4]

An equilateral triangle (Greek: ἰσόπλευρον, romanized: isópleuron, lit. 'equal sides') has three sides of the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°.^[5]
An isosceles triangle (Greek: ἰσοσκελὲς, romanized: isoskelés, lit. 'equal legs') has two sides of equal length.^{[note 1]}^[6] An isosceles triangle also has two angles of the same measure, namely the angles opposite to the two sides of the same length. This fact is the content of the isosceles triangle theorem, which was known by Euclid. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides.^[6] The latter definition would make all equilateral triangles isosceles triangles. The 45–45–90 right triangle, which appears in the tetrakis square tiling, is isosceles.
A scalene triangle (Greek: σκαληνὸν, romanized: skalinón, lit. 'unequal') has all its sides of different lengths.^[7] Equivalently, it has all angles of different measure.

Equilateral Triangle
Isosceles triangle
Scalene triangle

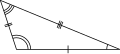
Hatch marks, also called tick marks, are used in diagrams of triangles and other geometric figures to identify sides of equal lengths.^[1] A side can be marked with a pattern of "ticks", short line segments in the form of tally marks; two sides have equal lengths if they are both marked with the same pattern. In a triangle, the pattern is usually no more than 3 ticks. An equilateral triangle has the same pattern on all 3 sides, an isosceles triangle has the same pattern on just 2 sides, and a scalene triangle has different patterns on all sides since no sides are equal.

Similarly, patterns of 1, 2, or 3 concentric arcs inside the angles are used to indicate equal angles: an equilateral triangle has the same pattern on all 3 angles, an isosceles triangle has the same pattern on just 2 angles, and a scalene triangle has different patterns on all angles, since no angles are equal.

By internal angles

The first page of Euclid's Elements, from the world's first printed version (1482), showing the "definitions" section of Book I. The right triangle is labeled "orthogonius", and the two angles shown are "acutus" and "angulus obtusus".

Triangles can also be classified according to their internal angles, measured here in degrees.

A right triangle (or right-angled triangle, formerly called a rectangled triangle) has one of its interior angles measuring 90° (a right angle). The side opposite to the right angle is the hypotenuse, the longest side of the triangle. The other two sides are called the legs or catheti^[8] (singular: cathetus) of the triangle. Right triangles obey the Pythagorean theorem: the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse: a² + b² = c², where a and b are the lengths of the legs and c is the length of the hypotenuse. Special right triangles are right triangles with additional properties that make calculations involving them easier. One of the two most famous is the 3–4–5 right triangle, where 3² + 4² = 5². The 3–4–5 triangle is also known as the Egyptian triangle.^[9] In this situation, 3, 4, and 5 are a Pythagorean triple. The other one is an isosceles triangle that has 2 angles measuring 45 degrees (45–45–90 triangle).
- Triangles that do not have an angle measuring 90° are called oblique triangles.
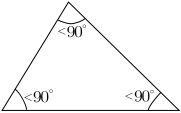
A triangle with all interior angles measuring less than 90° is an acute triangle or acute-angled triangle.^[3] If c is the length of the longest side, then a² + b² > c², where a and b are the lengths of the other sides.
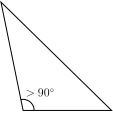
A triangle with one interior angle measuring more than 90° is an obtuse triangle or obtuse-angled triangle.^[3] If c is the length of the longest side, then a² + b² < c², where a and b are the lengths of the other sides.
A triangle with an interior angle of 180° (and collinear vertices) is degenerate. A right degenerate triangle has collinear vertices, two of which are coincident.

A triangle that has two angles with the same measure also has two sides with the same length, and therefore it is an isosceles triangle. It follows that in a triangle where all angles have the same measure, all three sides have the same length, and therefore is equilateral.


Right	Obtuse	Acute
	$\underbrace {\qquad \qquad \qquad \qquad \qquad \qquad } _{}$
	Oblique

Basic facts

A triangle, showing exterior angle d.

Triangles are assumed to be two-dimensional plane figures, unless the context provides otherwise (see Non-planar triangles, below). In rigorous treatments, a triangle is therefore called a 2-simplex (see also Polytope). Elementary facts about triangles were presented by Euclid, in books 1–4 of his Elements, written around 300 BC.

The measures of the interior angles of the triangle always add up to 180 degrees (same color to point out they are equal).

The sum of the measures of the interior angles of a triangle in Euclidean space is always 180 degrees.^[10]^[3] This fact is equivalent to Euclid's parallel postulate. This allows determination of the measure of the third angle of any triangle, given the measure of two angles. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles that are not adjacent to it; this is the exterior angle theorem. The sum of the measures of the three exterior angles (one for each vertex) of any triangle is 360 degrees.^{[note 2]}

Similarity and congruence

Two triangles are said to be similar, if every angle of one triangle has the same measure as the corresponding angle in the other triangle. The corresponding sides of similar triangles have lengths that are in the same proportion, and this property is also sufficient to establish similarity.

Some basic theorems about similar triangles are:

If and only if one pair of internal angles of two triangles have the same measure as each other, and another pair also have the same measure as each other, the triangles are similar.
If and only if one pair of corresponding sides of two triangles are in the same proportion as are another pair of corresponding sides, and their included angles have the same measure, then the triangles are similar. (The included angle for any two sides of a polygon is the internal angle between those two sides.)
If and only if three pairs of corresponding sides of two triangles are all in the same proportion, then the triangles are similar.^{[note 3]}

Two triangles that are congruent have exactly the same size and shape:^{[note 4]} all pairs of corresponding interior angles are equal in measure, and all pairs of corresponding sides have the same length. (This is a total of six equalities, but three are often sufficient to prove congruence.)

Some individually necessary and sufficient conditions for a pair of triangles to be congruent are:

SAS Postulate: Two sides in a triangle have the same length as two sides in the other triangle, and the included angles have the same measure.
ASA: Two interior angles and the included side in a triangle have the same measure and length, respectively, as those in the other triangle. (The included side for a pair of angles is the side that is common to them.)
SSS: Each side of a triangle has the same length as a corresponding side of the other triangle.
AAS: Two angles and a corresponding (non-included) side in a triangle have the same measure and length, respectively, as those in the other triangle. (This is sometimes referred to as AAcorrS and then includes ASA above.)

Some individually sufficient conditions are:

Hypotenuse-Leg (HL) Theorem: The hypotenuse and a leg in a right triangle have the same length as those in another right triangle. This is also called RHS (right-angle, hypotenuse, side).
Hypotenuse-Angle Theorem: The hypotenuse and an acute angle in one right triangle have the same length and measure, respectively, as those in the other right triangle. This is just a particular case of the AAS theorem.

An important condition is:

Side-Side-Angle (or Angle-Side-Side) condition: If two sides and a corresponding non-included angle of a triangle have the same length and measure, respectively, as those in another triangle, then this is not sufficient to prove congruence; but if the angle given is opposite to the longer side of the two sides, then the triangles are congruent. The Hypotenuse-Leg Theorem is a particular case of this criterion. The Side-Side-Angle condition does not by itself guarantee that the triangles are congruent because one triangle could be obtuse-angled and the other acute-angled.

Using right triangles and the concept of similarity, the trigonometric functions sine and cosine can be defined. These are functions of an angle which are investigated in trigonometry.

Right triangles

The Pythagorean theorem

A central theorem is the Pythagorean theorem, which states in any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides. If the hypotenuse has length c, and the legs have lengths a and b, then the theorem states that

$a^{2}+b^{2}=c^{2}.$

The converse is true: if the lengths of the sides of a triangle satisfy the above equation, then the triangle has a right angle opposite side c.

Some other facts about right triangles:

The acute angles of a right triangle are complementary.

$a+b+90^{\circ }=180^{\circ }\Rightarrow a+b=90^{\circ }\Rightarrow a=90^{\circ }-b.$

If the legs of a right triangle have the same length, then the angles opposite those legs have the same measure. Since these angles are complementary, it follows that each measures 45 degrees. By the Pythagorean theorem, the length of the hypotenuse is the length of a leg times √2.
In a right triangle with acute angles measuring 30 and 60 degrees, the hypotenuse is twice the length of the shorter side, and the longer side is equal to the length of the shorter side times √3:

$c=2a\,$

$b=a\times {\sqrt {3}}.$

For all triangles, angles and sides are related by the law of cosines and law of sines (also called the cosine rule and sine rule).

Existence of a triangle

Condition on the sides

The triangle inequality states that the sum of the lengths of any two sides of a triangle must be greater than or equal to the length of the third side. That sum can equal the length of the third side only in the case of a degenerate triangle, one with collinear vertices. It is not possible for that sum to be less than the length of the third side. A triangle with three given positive side lengths exists if and only if those side lengths satisfy the triangle inequality.

Conditions on the angles

Three given angles form a non-degenerate triangle (and indeed an infinitude of them) if and only if both of these conditions hold: (a) each of the angles is positive, and (b) the angles sum to 180°. If degenerate triangles are permitted, angles of 0° are permitted.

Trigonometric conditions

Three positive angles α, β, and γ, each of them less than 180°, are the angles of a triangle if and only if any one of the following conditions holds:

$\tan {\frac {\alpha }{2}}\tan {\frac {\beta }{2}}+\tan {\frac {\beta }{2}}\tan {\frac {\gamma }{2}}+\tan {\frac {\gamma }{2}}\tan {\frac {\alpha }{2}}=1,$ ^[11]

$\sin ^{2}{\frac {\alpha }{2}}+\sin ^{2}{\frac {\beta }{2}}+\sin ^{2}{\frac {\gamma }{2}}+2\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}=1,$ ^[11]

$\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )=4\sin(\alpha )\sin(\beta )\sin(\gamma ),$

$\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma +2\cos(\alpha )\cos(\beta )\cos(\gamma )=1,$ ^[12]

$\tan(\alpha )+\tan(\beta )+\tan(\gamma )=\tan(\alpha )\tan(\beta )\tan(\gamma ),$

the last equality applying only if none of the angles is 90° (so the tangent function's value is always finite).

Note:–

* It is one of the basic shapes in geometry.

* A Triangle has three angles so it is called Triangle (with three angles).

* A Triangle has three sides so it may be called Trigon. (with three angles).

* Contents of Triangle

A triangle consists of various parts. It has 3 sides, 3 vertices and 3 angles.

1. Vertexes :- The corner or meeting point of the two sides of triangle is called vertexs of triangle.

There are three vertices in a triangle which is denoted by capital letters, A, B and C.

Vertexes

1. Vertex 1 :- A

2. Vertex 2 :- B

3. Vertex 3 :- C

2. Sides :- The line joining the two vertexes of triangle is called Sides of triangle.

There are three Sides in a triangle which is denoted by capital letters, AB or BA, BC or CB and CA or AC.

Sides

1. Side 1 :- AB or BA

2. Side 2 :- BC or CB

3. Side 3 :- CA or AC

Vertex of triangle is denoted by capital letters, A, B and C.

3. Angles :- The depression between two sides at a vertex is called Angle.

There are three Angles in a triangle which is denoted by the symbol of angle (∠).

It is denoted in three ways

∠A or AB or BA, AB or BC or CB and AB or CA or AC.

Sides

1. Angle 1 :- ∠A or ∠BAC or ∠CAB

2. Angle 2 :- ∠B or ∠ABC or ∠CBA

3. Angle 3 :- ∠C or ∠ACB or ∠BCA

In this the desired angle is written in between ∠A or ∠BAC or ∠CAB

Triangle 2