पिरामिड एक 3D आकृति है जो एक बहुभुज के आधार और सभी त्रिकोणीय चेहरों को एक साथ जोड़कर बनाई गई है। एक पिरामिड आधार के प्रत्येक शीर्ष को एक सामान्य सिरे या शीर्ष से जोड़ता है और इसे विशिष्ट आकार देता है। आइए इस अनुभाग में पिरामिडों के बारे में और जानें।
पिरामिड की परिभाषा
पिरामिड एक 3D बहुफलक है जिसका आधार एक बहुभुज के साथ-साथ तीन या अधिक त्रिभुज-आकार के फलक होते हैं जो आधार के ऊपर एक बिंदु पर मिलते हैं। त्रिकोणीय भुजाओं को फलक कहा जाता है और आधार के ऊपर के बिंदु को शीर्ष कहा जाता है। आधार को शीर्ष से जोड़कर पिरामिड बनाया जाता है। कभी-कभी, त्रिकोणीय भुजाओं को आधार से अलग करने के लिए पार्श्व फलक भी कहा जाता है। पिरामिड में, आधार का प्रत्येक किनारा शीर्ष से जुड़ा होता है जो त्रिकोणीय चेहरा बनाता है।

पिरामिड के गुण
यहां पिरामिड के विभिन्न गुणों की एक सूची दी गई है जो हमें इसे आसानी से पहचानने में मदद करती है:
- पिरामिड तीन मुख्य भागों से बना होता है - शीर्ष, फलक और आधार।
- बहुभुज का आधार प्रायः वर्ग के आकार का होता है।
- आधार को छोड़कर पिरामिड के सभी फलकों को पार्श्व फलक कहा जाता है।
- यदि आधार एक नियमित बहुभुज है, तो त्रिभुज सर्वांगसम और समद्विबाहु त्रिभुज होते हैं ।
- दो प्रतिच्छेदी फलकों द्वारा बनाए गए रेखाखंडों को किनारा कहा जाता है और वह बिंदु या कोना जिस पर तीन या अधिक किनारे मिलते हैं उसे शीर्ष कहा जाता है।
- शीर्ष वह शीर्ष है जो आधार के विपरीत है और पिरामिड को आकार देता है।
पिरामिड के प्रकार
आधार के आकार के आधार पर पिरामिड विभिन्न प्रकार के होते हैं । आइए विभिन्न प्रकार के पिरामिडों पर नजर डालें:
चौकोर पिरामिड
एक वर्गाकार पिरामिड तब बनता है जब पिरामिड का आधार वर्गाकार होता है। एक वर्गाकार पिरामिड में एक वर्गाकार आधार और तीन त्रिकोणीय फलक होते हैं। दूसरे शब्दों में, इसके 8 किनारे, 5 शीर्ष और 4 फलक हैं। इसके आकार को समझने के लिए नीचे दिखाए गए वर्गाकार पिरामिड को देखें।

त्रिकोणीय पिरामिड
यदि किसी पिरामिड का आधार त्रिभुज के आकार का हो तो उसे त्रिभुजाकार पिरामिड कहा जाता है । एक त्रिकोणीय पिरामिड में 4 फलक, 6 किनारे और 4 शीर्ष होते हैं। इस प्रकार के पिरामिड को चतुष्फलक भी कहा जा सकता है। इसके आकार को समझने के लिए नीचे दिखाए गए त्रिकोणीय पिरामिड को देखें।

पंचकोणीय पिरामिड
पंचकोणीय पिरामिड वह होता है जिसका आधार पंचकोण के आकार का होता है, और शेष फलक त्रिभुज के रूप में होते हैं। इस पिरामिड में 6 फलक, 6 शीर्ष और 10 किनारे हैं। इसके आकार की बेहतर समझ के लिए निम्नलिखित पंचकोणीय पिरामिड का अवलोकन करें।

दायां पिरामिड बनाम तिरछा पिरामिड
पिरामिड के शीर्ष या शीर्ष का स्थान यह तय करता है कि पिरामिड एक सीधा पिरामिड है या तिरछा पिरामिड है। एक पिरामिड को दायीं पिरामिड का नाम दिया जाता है जब शीर्ष का स्थान पिरामिड के आधार के बिल्कुल मध्य में होता है। वहीं, जब शीर्ष का स्थान बिल्कुल मध्य के ऊपर न होकर थोड़ा दूर हो तो उस पिरामिड को तिरछा पिरामिड कहा जाता है। दूसरे शब्दों में, जब शीर्ष से एक लंबवत रेखा आधार के केंद्र को काटती है, तो यह एक सही पिरामिड है। जब यह आधार के केंद्र को नहीं काटता है, तो यह एक तिरछा पिरामिड होता है। तिरछे पिरामिड और दाएं पिरामिड के बीच अंतर देखने के लिए निम्नलिखित आंकड़ों पर गौर करें।

नियमित बनाम अनियमित पिरामिड
यदि पिरामिड का आधार एक नियमित बहुभुज है, तो इसे एक नियमित पिरामिड माना जाता है। यदि आधार एक अनियमित बहुभुज है, जहां भुजाएं एक दूसरे के बराबर नहीं हैं, तो यह एक अनियमित पिरामिड है। नियमित और अनियमित पिरामिड के बीच अंतर जानने के लिए निम्नलिखित चित्र को देखें।

पिरामिड का आयतन
पिरामिड का आयतन उसके चेहरों के बीच घिरे स्थान को दर्शाता है । पिरामिड के आधार के आधार पर प्रत्येक पिरामिड का एक अलग सूत्र होता है। पिरामिड का आयतन घन इकाइयों में मापा जाता है और पिरामिड के आयतन की गणना के लिए उपयोग किया जाने वाला सूत्र है: पिरामिड का आयतन = 1/3 × आधार क्षेत्रफल × ऊँचाई
पिरामिड का सतही क्षेत्रफल
विभिन्न प्रकार के पिरामिडों के लिए पिरामिड का सतह क्षेत्र अलग-अलग होता है। पिरामिड का सतह क्षेत्रफल ज्ञात करने के लिए उपयोग किया जाने वाला सूत्र इस प्रकार है:
जब सभी पार्श्व फलक समान हों, तो सूत्र है: सतह क्षेत्र = आधार क्षेत्र + (½ × आधार का परिमाप × तिरछी ऊंचाई)
जब पार्श्व फलक भिन्न होते हैं, तो सूत्र होता है: सतह क्षेत्र = आधार क्षेत्र + पार्श्व क्षेत्र
यह ध्यान दिया जाना चाहिए कि जब पार्श्व फलक भिन्न होते हैं, जैसे कि अनियमित पिरामिड के मामले में, हम प्रत्येक त्रिभुज के क्षेत्रफल को जोड़कर कुल पार्श्व क्षेत्रफल की गणना करते हैं।
पिरामिड का जाल
विभिन्न प्रकार के पिरामिडों को चपटा करके खोलने पर पिरामिड का जाल दिखाई देता है। उदाहरण के लिए, एक वर्गाकार पिरामिड के जाल में एक वर्ग के आकार का आधार और 4 त्रिभुज भुजाएँ या फलक होते हैं। एक त्रिकोणीय पिरामिड के जाल में 5 फलक होते हैं, अर्थात, एक वर्गाकार आधार और 4 त्रिकोणीय पार्श्व फलक। पिरामिड का जाल देखने के लिए निम्नलिखित आकृति का अवलोकन करें।

पिरामिड पर उदाहरण
उदाहरण 1: पिरामिड का आयतन ज्ञात कीजिए, यदि इसका आधार क्षेत्रफल 60 इकाई 2 है और इसकी ऊँचाई 12 इकाई है।
समाधान: आधार क्षेत्रफल = 60 और ऊंचाई = 12
आइए सूत्र में मानों को प्रतिस्थापित करके आयतन की गणना करें।
पिरामिड का आयतन = 1/3 × आधार क्षेत्रफल × ऊँचाई
आयतन = 1/3 × 60 × 12
Volume = 240 units3
Therefore, the volume of the pyramid is 240 units3
Example 2: Find the surface area of a square pyramid with the given dimensions: side of the base = 16 inches, slant height = 15 inches.
Solution: The perimeter of the base = 4 × 16 = 64 inches; Base area = a2 = 162 = 256 square inches; slant height = 15 inches
Let us fill in all the dimensions in the formula:
Surface Area = Base Area + (½ × Perimeter of the base × Slant height)
Surface area = 256 + (½ × 64 × 15)
Surface area = 736 inch2
Therefore, the surface area of the square pyramid is 736 inch2
Example 3: State true or false.
a.) The net of a square pyramid consists of a base with the shape of a square along with 4 triangle sides or faces.
b.) Apex is the vertex that is opposite to the base and gives the shape to the pyramid.
Solution:
a.) True, the net of a square pyramid consists of a base with the shape of a square along with 4 triangle sides or faces.
b.) True, the apex is the vertex that is opposite to the base and gives the shape to the pyramid.
Practice Questions on Pyramid
प्र.1
यदि शीर्ष आधार के मध्य के ठीक ऊपर स्थित नहीं है, तो यह किस प्रकार का पिरामिड है?
जवाबप्रश्न 2:
यदि पिरामिड का आधार एक नियमित बहुभुज है, तो पिरामिड एक अनियमित पिरामिड है। यह कथन सही है या गलत?
जवाब
from a handpicked teacher in LIVE 1-to-1 classes
Volume of Triangular Prism
The volume of a triangular prism is the space occupied by it from all three dimensions. A prism is a solid object which has identical bases, flat rectangular side faces, and the same cross-section all along its length. There are different types of prisms that are classified and named as per the shape of their base. A triangular prism has 2 identical triangular bases and 3 rectangular lateral faces.
The volume of a triangular prism is the space occupied by it from all three dimensions. A prism is a solid object which has identical bases, flat rectangular side faces, and the same cross-section all along its length. There are different types of prisms that are classified and named as per the shape of their base. A triangular prism has 2 identical triangular bases and 3 rectangular lateral faces.
What is the Volume of a Triangular Prism?
The volume of a triangular prism can be calculated by taking the product of the area of the triangular base and the height of the prism which is also known as the length of the prism. For this, let us first understand what a triangular prism looks like.
The volume of a triangular prism can be calculated by taking the product of the area of the triangular base and the height of the prism which is also known as the length of the prism. For this, let us first understand what a triangular prism looks like.
Definition of Triangular Prism
A triangular prism is a polyhedron made up of two triangular bases and three rectangular sides. Or, it can be considered as a pentahedron (as it has 5 faces altogether) wherein the edges and vertices of the bases are joined with each other by three rectangular sides. By definition, the two triangular bases are parallel and congruent to each other. It has:
- 2 bases (which are congruent triangles)
- 3 side faces (which are congruent rectangles)
- Total number of faces - 5
- 9 edges
- 6 corners or vertices
The length of the triangular prism is the perpendicular distance between the centers of the two bases. It is represented by "l" in the figure given below.
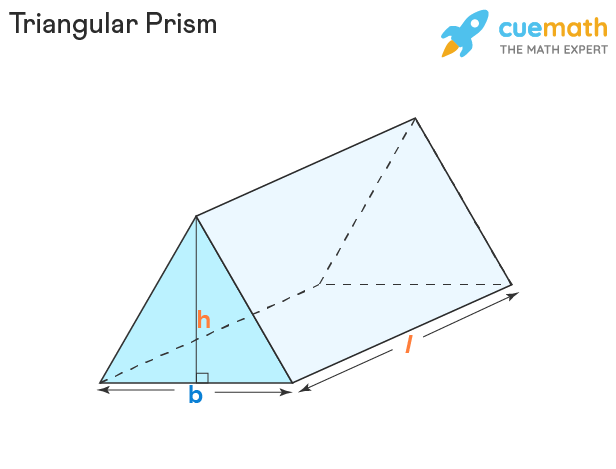
Observe the triangular prism shown above where 'b' is the base of each side of two congruent triangles, 'h' is the height of the base triangle, and 'l' is the length of the prism.
A triangular prism is a polyhedron made up of two triangular bases and three rectangular sides. Or, it can be considered as a pentahedron (as it has 5 faces altogether) wherein the edges and vertices of the bases are joined with each other by three rectangular sides. By definition, the two triangular bases are parallel and congruent to each other. It has:
- 2 bases (which are congruent triangles)
- 3 side faces (which are congruent rectangles)
- Total number of faces - 5
- 9 edges
- 6 corners or vertices
The length of the triangular prism is the perpendicular distance between the centers of the two bases. It is represented by "l" in the figure given below.

Observe the triangular prism shown above where 'b' is the base of each side of two congruent triangles, 'h' is the height of the base triangle, and 'l' is the length of the prism.
Volume of Triangular Prism Formula
The volume of a triangular prism is the space inside it or the space occupied by it. It is measured in cubic units such as cm3, m3, in3, etc. We will see the formulas to calculate the volumes of different types of triangular prisms. The volume of any prism is obtained by multiplying its base area by its length.
The volume of a prism = base area × length of the prism
We will use this formula to calculate the volume of a triangular prism as well. We know that the base of a triangular prism is a triangle. By applying the above formula to a triangular prism, we get,
The volume of a triangular prism is the space inside it or the space occupied by it. It is measured in cubic units such as cm3, m3, in3, etc. We will see the formulas to calculate the volumes of different types of triangular prisms. The volume of any prism is obtained by multiplying its base area by its length.
The volume of a prism = base area × length of the prism
We will use this formula to calculate the volume of a triangular prism as well. We know that the base of a triangular prism is a triangle. By applying the above formula to a triangular prism, we get,
Volume of a triangular prism = area of base triangle × length of the prism
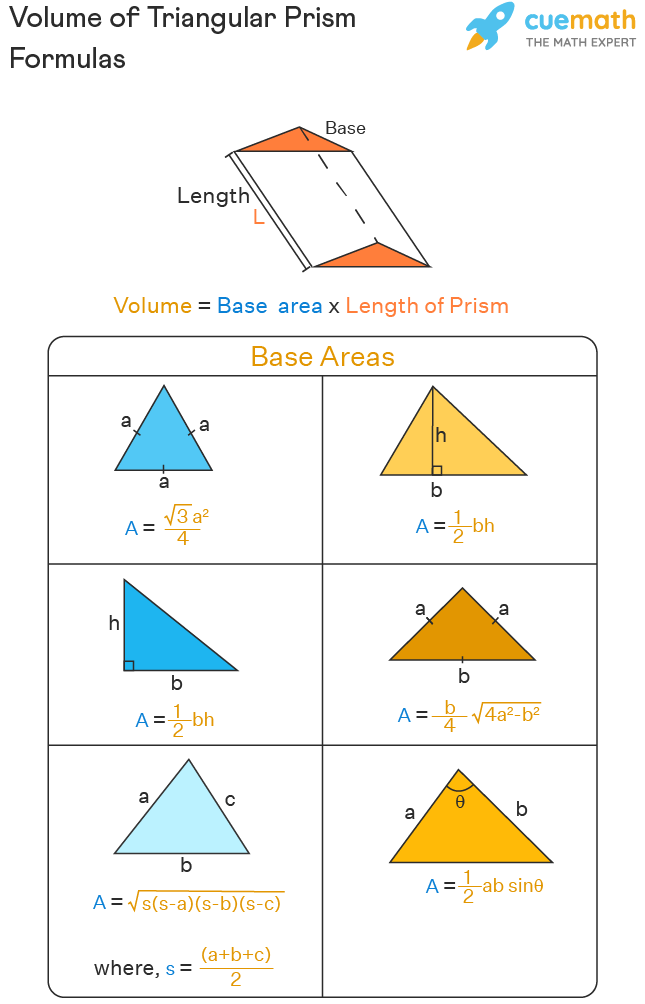
Here, we can find the area of the base triangle based on its type and the available information. The following list shows the formulas to find the area of the base triangle.
- If the base triangle is an equilateral triangle (in this case, the prism is called equilateral triangular prism) with each side 'a', then its area = √3a2/4
- If the triangle's base 'b' and height 'h' are given, then its area = (1/2) bh
- If the base triangle is a right-angled triangle (in this case, the prism is called a right triangular prism) with two legs 'b' and 'h' then its area = (1/2) bh
- If the base triangle is an isosceles triangle with its sides to be 'a', 'a', and 'b' then its area is (b/4) × √(4a2 - b2)
- If the base triangle is a scalene triangle where all three sides 'a', 'b', and 'c' are given, then its area is calculated using √[s(s-a)(s-b)(s-c)]; where, s = (a + b + c)/2. Note that you can apply this formula (which is also called Heron's formula) for an isosceles triangle (or) an equilateral triangle as well.
- If the base triangle's two sides 'a' and 'b' and the included angle 'θ' are given, then its area is found using 1/2 ab sin θ
Here, we can find the area of the base triangle based on its type and the available information. The following list shows the formulas to find the area of the base triangle.
- If the base triangle is an equilateral triangle (in this case, the prism is called equilateral triangular prism) with each side 'a', then its area = √3a2/4
- If the triangle's base 'b' and height 'h' are given, then its area = (1/2) bh
- If the base triangle is a right-angled triangle (in this case, the prism is called a right triangular prism) with two legs 'b' and 'h' then its area = (1/2) bh
- If the base triangle is an isosceles triangle with its sides to be 'a', 'a', and 'b' then its area is (b/4) × √(4a2 - b2)
- If the base triangle is a scalene triangle where all three sides 'a', 'b', and 'c' are given, then its area is calculated using √[s(s-a)(s-b)(s-c)]; where, s = (a + b + c)/2. Note that you can apply this formula (which is also called Heron's formula) for an isosceles triangle (or) an equilateral triangle as well.
- If the base triangle's two sides 'a' and 'b' and the included angle 'θ' are given, then its area is found using 1/2 ab sin θ

the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
How to Find the Volume of Triangular Prism?
The volume of a triangular prism can be calculated with the help of the following steps and the example given below. Before that make sure that all measurements are of the same units
Step 1: Identify the type of the base triangle and find its area using a suitable formula (as explained in the previous section).
Step 2: Identify the length of the prism (Note that this length of the prism is also known as the height of the prism, and it should not be confused with the height of the base triangle).
Step 3: Multiply the base area (from step 1) and the length of the prism to find the volume.
Example: Calculate the volume of the triangular prism whose length is 15 in and whose base is an equilateral triangle of side 6 inches.
Solution: The volume of the triangular prism can be calculated using the following steps.
Step 1: The base triangle is an equilateral triangle with its side as a = 6. So its area is found using the formula, √3a2/4 = √3(6)2/4 = 9√3 square inches.
Step 2: The length of the prism is 15 in.
Step 3: The volume of the given triangular prism = base area × length = 9√3 × 15 = 135√3 cubic inches.
Tips on Volume of Triangular Prism
The length of a triangular prism is also known as the height of the prism.
This height of the prism should not be confused with the height of the base triangle.
☛
☛
Pyramid
A pyramid is a 3D figure built with a base of a polygon and triangular faces all connected together. A pyramid connects each vertex of the base to a common tip or apex giving it the typical shape. Let us learn more about pyramids in this section.
Definition of Pyramid
A pyramid is a 3D polyhedron with the base of a polygon along with three or more triangle-shaped faces that meet at a point above the base. The triangular sides are called faces and the point above the base is called the apex. A pyramid is made by connecting the base to the apex. Sometimes, the triangular sides are also called lateral faces to distinguish them from the base. In a pyramid, each edge of the base is connected to the apex that forms the triangular face.

Properties of a Pyramid
Here is a list of the different properties of a pyramid that help us to identify it easily:
- A pyramid is made of three main parts - apex, face, and base.
- The polygon base is most often in the shape of a square.
- The faces of the pyramid except the base are called lateral faces.
- If the base is a regular polygon, the triangles are congruent and isosceles triangles.
- The line segments created by two intersecting faces are called edges and the point or corner at which three or more edges meet is the vertex.
- Apex is the vertex that is opposite to the base and gives the shape to the pyramid.
Types of Pyramids
There are different types of pyramids based on the shape of their base. Let us look at the different types of pyramids:
Square Pyramid
A square pyramid is formed when the base of the pyramid is in the shape of a square. A square pyramid consists of one square base and three triangular faces. In other words, it has 8 edges, 5 vertices, and 4 faces. Observe the square pyramid shown below to understand its shape.

Triangular Pyramid
If the base of a pyramid is in the shape of a triangle, it is said to be a triangular pyramid. A triangular pyramid has 4 faces, 6 edges, and 4 vertices. This kind of pyramid can also be called a tetrahedron. Observe the triangular pyramid shown below to understand its shape.

Pentagonal Pyramid
A pentagonal pyramid is one that has its base shaped like a pentagon, with the rest of the faces as triangles. This pyramid has 6 faces, 6 vertices, and 10 edges. Observe the following pentagonal pyramid for a better understanding of its shape.

Right Pyramid vs Oblique Pyramid
The location of the apex or the top of a pyramid decides whether a pyramid is a right pyramid or an oblique pyramid. A pyramid is named as a right pyramid when the location of the apex is exactly over the middle of the base of the pyramid. Whereas, when the location of the apex is not exactly over the middle but slightly away, then that pyramid is called an oblique pyramid. In other words, when a perpendicular line from the apex intersects the centre of the base, it is a right pyramid. When it does not intersect the center of the base, it is an oblique pyramid. Observe the following figures to see the difference between an oblique pyramid and a right pyramid.

Regular vs Irregular Pyramid
If the base of the pyramid is a regular polygon, it is considered to be a regular pyramid. If the base is an irregular polygon, where the sides are not equal to each other, then it is an irregular pyramid. Observe the following figure to notice the difference between a regular and an irregular pyramid.

Volume of a Pyramid
The volume of a pyramid refers to the space enclosed between its faces. Each pyramid has a different formula depending on the base of the pyramid. The volume of a pyramid is measured in cubic units and the formula used to calculate the volume of a pyramid is: Volume of a Pyramid = 1/3 × Base Area × Height
Surface Area of a Pyramid
The surface area of a pyramid is different for different types of pyramids. The formula used to find the surface area of a pyramid is as follows:
When all side faces are the same, the formula is: Surface Area = Base Area + (½ × Perimeter of the base × Slant height)
When side faces are different, the formula is: Surface Area = Base Area + Lateral Area
It should be noted that when the side faces are different, as in the case of irregular pyramids, we calculate the total lateral area by adding the area of each triangle.
Net of a Pyramid
The net of a pyramid is seen when the different types of pyramids are flattened and opened up. For example, the net of a square pyramid consists of a base with the shape of a square along with 4 triangle sides or faces. The net of a triangular pyramid consists of 5 faces, i.e., one square base and 4 triangular lateral faces. Observe the following figure to see the net of a pyramid.

☛
Example 1: Find the volume of the pyramid, if its base area is 60 unit2 and its height is 12 units.
Solution: Base area = 60 and height = 12
Let us calculate the volume by substituting the values in the formula.
Volume of a pyramid = 1/3 × Base Area × Height
Volume = 1/3 × 60 × 12
Volume = 240 units3
Therefore, the volume of the pyramid is 240 units3
Example 2: Find the surface area of a square pyramid with the given dimensions: side of the base = 16 inches, slant height = 15 inches.
Solution: The perimeter of the base = 4 × 16 = 64 inches; Base area = a2 = 162 = 256 square inches; slant height = 15 inches
Let us fill in all the dimensions in the formula:
Surface Area = Base Area + (½ × Perimeter of the base × Slant height)
Surface area = 256 + (½ × 64 × 15)
Surface area = 736 inch2
Therefore, the surface area of the square pyramid is 736 inch2
Example 3: State true or false.
a.) The net of a square pyramid consists of a base with the shape of a square along with 4 triangle sides or faces.
b.) Apex is the vertex that is opposite to the base and gives the shape to the pyramid.
Solution:
a.) True, the net of a square pyramid consists of a base with the shape of a square along with 4 triangle sides or faces.
b.) True, the apex is the vertex that is opposite to the base and gives the shape to the pyramid.
Practice Questions on Pyramid
Q.1
If the apex is not located exactly above the middle of the base, what type of pyramid is it?
Responses
Rectangular Prism
A rectangular prism is a three-dimensional shape, having six faces, where all the faces (top, bottom, and lateral faces) of the prism are rectangles such that all the pairs of the opposite faces are congruent. Like all three-dimensional shapes, a rectangular prism also has volume and surface area. A rectangular prism is also known as a cuboid. Let us learn more about a rectangular prism along with the formulas to find its volume and surface area.
What is a Rectangular Prism?
A rectangular prism is a prism whose bases (the top face and the bottom face) are also rectangles. It has 6 faces in all, out of which there are 3 pairs of identical opposite faces, i.e., all the opposite faces are identical in a rectangular prism. It has three dimensions, length, width, and height. Some examples of a rectangular prism in real life are rectangular tissue boxes, school notebooks, laptops, fish tanks, large structures such as cargo containers, rooms, storage sheds, etc. The following figure shows a rectangular prism and its net, which is a two-dimensional representation of the prism when its faces are opened on a 2D plane.

Faces Edges Vertices of a Rectangular Prism
A rectangular prism has 6 faces, 12 edges (sides) and 8 vertices (corners). In the 12 edges, 3 edges intersect to form right angles at each vertex.
Types of Rectangular Prisms
There are two types of rectangular prisms that are classified depending on the shape of the faces or the angle made by the faces with the base.
- Right rectangular prism: In a right rectangular prism, the faces are perpendicular to each of its bases. In this, all side faces are rectangles.
- Oblique rectangular prism: In an oblique rectangular prism, the faces are not perpendicular to the bases. In other words, the faces in this prism are parallelograms.
In general, a rectangular prism without any specifications is a right rectangular prism.

Properties of Rectangular Prism
The properties of a rectangular prism are given below which help us to identify it easily.
- A rectangular prism has 6 faces, 8 vertices, and 12 edges.
- In a right rectangular prism, the faces are rectangles, whereas, in an oblique rectangular prism, the faces are parallelograms.
- It has 3 dimensions which are length, width, and height.
- The opposite faces of a rectangular prism are congruent.
Rectangular Prism Formulas
In this section, we will learn the formulas of the volume and surface area of a rectangular prism. For both of these, let us consider a rectangular prism of length 'l', width 'w', and height 'h'. Along these dimensions, let us assume that 'l' and 'w' are the dimensions of the base. Here are the formulas for the volume and surface area of a rectangular prism.
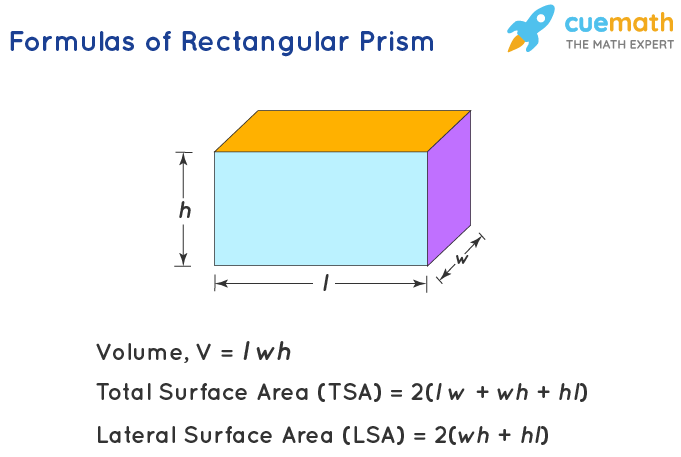
Let us see how to derive these formulas.
Volume of Rectangular Prism
The volume of a rectangular prism is the space that is inside it. We know that the volume of any prism is obtained by multiplying its base area by its height. Here,
- The base area of the rectangular prism = lw (using the area of a rectangle formula)
- The height of the rectangular prism = h
Thus, the volume of the rectangular prism, V = lw × h = lwh.
Surface Area of Rectangular Prism
There are two types of surface areas of a rectangular prism, one is the total surface area (TSA) and the other is the lateral surface area (LSA).
- The total surface area of a rectangular prism is the sum of the areas of all of its faces.
- The lateral surface area of a rectangular prism is the sum of the areas of all its side faces (excluding the bases).
We can calculate the areas of the side faces of a rectangular prism using its net.
The total surface area (TSA) of a rectangular prism
= The sum of areas of all faces
= lw + lw + wh + wh + hl + hl
= 2 (lw + wh + hl)
The lateral surface area (LSA) of a rectangular prism
= The sum of areas of side faces
= wh + wh + hl + hl
= 2 (wh + hl)
We will see the applications of these volume and surface area formulas of a rectangular prism in the section of Rectangular Prism Examples given below.
Right Rectangular Prism
A right rectangular prism is a three-dimensional solid shape with 6 faces, 12 edges, and 8 vertices. It is also called a cuboid. The six faces of a right rectangular prism are rectangular in shape. Some examples of a right rectangular prism are books, aquarium, bricks. Similar to other two-dimensional and three-dimensional shapes, the right rectangular prism also has a surface area.
Right Rectangular Prism Definition
A right rectangular prism is a three-dimensional shape with six faces (with all the 6 faces being rectangular in shape), 12 edges and 8 vertices. All the faces of the prism are rectangles. All the angles formed at the vertices are of 90° or right angles.
Properties of a Right Rectangular Prism
It is very easy to identify a right rectangular prism if we know its basic properties. Listed below are its properties.
- The angles between the base and the sides are right angles.
- All its faces are rectangles.
- Each corner of the prism represents a right angle.
- Each base and top of the prism are congruent.
Formulas of a Right Rectangular Prism
To find the surface area, volume, and length of the diagonal of a right rectangular prism, it is easy if we apply some formulae to make our calculations easier. Let us learn about each of the formulas related to the right rectangular prism in this section.
Surface Area of a Right Rectangular Prism
Surface area is the space occupied by the outer surface of any solid shape. The surface area of a right rectangular prism is the space occupied by all the faces of the right rectangular prism.
Surface area of a right rectangular prism = lw+lw+wh+wh+lh+lh, which is equal to 2(lw+wh+lh) square units.

Surface Area = 2(lw+wh+lh) square units.
Volume of Right Rectangular Prism
Volume is the space occupied by a closed surface of a solid shape. Volume of a right rectangular prism can be defined as the product of the area of one face multiplied by its height.

The volume of a right rectangular prism (V) for a length (l), height (h), and width (w) is given by,
Volume = (l × w × h) cubic units.
Diagonal of a Right Rectangular Prism
A diagonal is a line that joins two opposite corners of a shape that has straight sides. The diagonal of a right rectangular prism is the square root of the sum of the squares of the length, width, and height.

The diagonal of a right rectangular prism of length (l), width (w), and height (h) is given by,
Diagonal = √l2+w2+h2
Important Notes
- A rectangular prism has six faces - the base, the top, and the four sides.
- The base and top always have the same area. The pairs of opposite sides have the same area as well.
- The volume of Rectangular Prism: V = lwh
- Surface Area of Rectangular Prism: S = 2(lw + lh + wh)
- In a right rectangular prism, edges = 12, faces = 6, vertices = 8
- When all sides of a right rectangular prism are equal, it is called a cube. Its surface area is 6a2 and volume is a3.
Challenging Questions
- Is a cube a rectangular prism?
- Can you determine the volume of a rectangular prism when the area of its base and height are given but the length and width are not given as separate measurements?
Rectangular Prism Net
A net is defined as a model of a two-dimensional shape that can be folded and made into a three-dimensional shape. The net of any geometrical three-dimensional shape is obtained by unfolding it along its edges and faces. The net of the right rectangular prism is equal to its surface area. The image given below shows the net of a rectangular prism. We can clearly observe that it is made up of rectangles. By calculating the area of each rectangle, and adding them up we can find the net or the surface area of the right rectangular prism.
Topics Related to Right Rectangular Prism
Check out these interesting articles to know more about right rectangular prism.
from a handpicked teacher in LIVE 1-to-1 classes
Square prism
A square prism is a three-dimensional cuboid in which the bases are squares. It has six faces in which two opposite faces are square in shape while the other four are rectangular. It should be noted that all square prisms are not cubes but all cubes are square prisms because cubes fulfill the properties of square prisms. Let us understand more about square prisms.
Definition of a Square Prism
A square prism is a three-dimensional cuboid where the base and top are equal squares and the remaining 4 faces are rectangles. The opposite sides and angles of a square prism are congruent and parallel to each other. A square prism has at least two of its length equal to each other. A real-life example is a tissue box that we see in our daily life.

Properties of Square Prism
A square prism has two ends as faces shaped like a square with 4 rectangles or squares in between them as other faces. Let us look at the various properties of a square prism:
- A square prism has 6 faces, 8 vertices, and 12 edges.
- The opposite sides of a square prism are parallel to each other.
- The opposite sides of a square prism are congruent to each other.
- In a square prism, the diagonals bisect each other.
- In a square prism, opposite angles are congruent to each other.
Types of Square Prisms
A square prism can be classified into two types. Let us learn the types in detail.
Right Square Prism
If the lateral faces of a square prism are aligned in one direction to its base, then it is termed as a right square prism. In other words, if the lateral faces are perpendicular to the base of the prism then the prism is a right square prism.
Oblique Square Prism
If the lateral faces of a prism are not perpendicular to the base of the prism, then it is known as an oblique square prism. Observe the following figure to note the difference between a right square prism and an oblique square prism.

Square Prism Formulas
There are two basic formulas related to the square prism:
- Surface area of a square prism.
- Volume of a square prism.
Surface area of square prism: If the length of the side of the square and height of a square prism is given, then its total surface area can be calculated with the help of the following formulas:
- The total surface area of a square prism = (2 × Base Area) + Lateral Surface Area
- This can be written as: (2 × a2) + (4 × a × h) = 2a2 + 4ah (where 'a' is the length of the side of the square and 'h' is the height of the square prism.)
Volume of a square prism: The amount of space occupied by a 3-dimensional prism is known as its volume and it is measured in cubic units.
- The volume of a prism is its cross-sectional area multiplied by its length. In other words, the volume of a square prism is its base area multiplied by its height.
- This can be written as: a2 h (where, a = side of a square prism, a2 = base area, h = height of the square prism)

Square Prism Net
A square prism net is when the solid shape is flattened by opening the prism entirely. The view of the square prism net provided us the accurate shapes of the 2 square faces along with 4 rectangle faces. When all flattened ends are combined together, we get the shape of a square prism. The image below shows the net of the square prism.

Related Articles on Square Prism
Check out the important topics mentioned below to learn more about square prism and its related terminologies.
- Rectangular Prism
- Surface Area of Rectangular Prism
- Pentagonal Prism
- Square Prism Formula
- Volume of Triangular Prism
from a handpicked teacher in LIVE 1-to-1 classes
Surface Area of Rectangular Prism
The surface area of a rectangular prism is the total area or region covered by its six faces. If l, b, and h are the length, breadth, and height of a rectangular prism, then:
- Its total surface area (TSA) = 2(lb + bh + lh)
- Its lateral surface area (LSA) = 2h (l + b)
Prisms are solids with flat parallelogram sides and identical polygon bases. There are different types of prisms, namely - triangular prisms, square prisms, rectangular prisms, pentagonal prisms, hexagonal prisms, etc. In this article, you will learn more about the surface area of rectangular prisms.
What is Surface Area of a Rectangular Prism?
The total region or area covered by all the faces of a rectangular prism is defined as the surface area of a rectangular prism. A rectangular prism is a three-dimensional shape. It has six faces, and all the faces are rectangular shaped. Therefore, both the bases of a rectangular prism must also be rectangles. For example, we can relate the surface area of a rectangular prism with the surfaces of the objects given below: a book, a cuboid-shaped aquarium, a box, etc.

For example, let's say there is a box that needs to be gift-wrapped. You need to calculate the amount of wrapping paper that will be needed to cover it. First, you will need to know the sum of the areas of the six surfaces of the box (four lateral side surfaces, top surface, and bottom surface). This total area of the six surfaces is called the surface area of a rectangular prism.
A rectangular prism can be classified as a right rectangular prism or an oblique rectangular prism. In the right rectangular prism, bases are perpendicular to each other whereas, in an oblique rectangular prism, the bases are not aligned one above the other. Let us see the basic formulas to calculate the total surface area and lateral surface area of a rectangular prism in the next section.
Surface Area of Rectangular Prism Formula
To calculate the surface area of a rectangular prism, we need to simply find the sum of the areas of the faces of the prism. A rectangular prism can have two types of areas:
- Total Surface Area (TSA)
- Lateral Surface Area (LSA)
Total Surface Area of Rectangular Prism
The total surface area of a rectangular prism can be calculated by finding the total area of all six faces. The formula to find the surface area of a rectangular prism is given as,
Total surface area of a rectangular prism = 2(lb + bh + lh) square units
where,
- l = Length of the rectangular prism
- b = Breadth of the rectangular prism
- h = Height of the rectangular prism
☛Note: The unit of measurement of the area of the rectangular prism is square units.
Lateral Surface Area of a Rectangular Prism
The lateral surface area of a rectangular prism can be calculated by finding the sum of all the lateral faces of the prism, i.e. the total area excluding the area of the bases. The formula to find the surface area of a rectangular prism is given as,
Lateral surface area of a rectangular prism = 2(l + b) h square units
where,
- l = Length
- b = Breadth
- h = Height of the rectangular prism
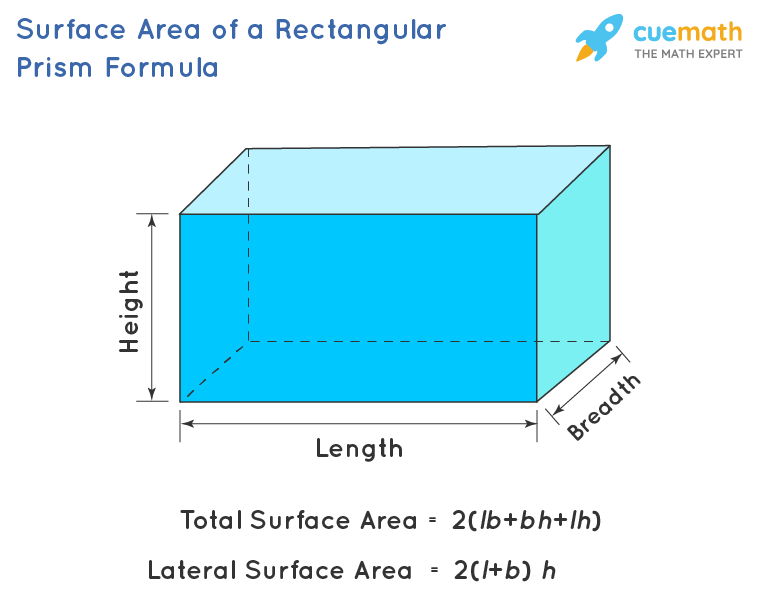
Example: Determine the total surface area of a rectangular prism with the following dimensions: Length (l) = 8 inches; Breadth (b) = 5 inches; Height (h) = 7 inches.
Solution: The total surface area of the rectangular prism is given by: 2(lb + bh + lh) = 2(8 × 5 + 5 × 7 + 8 × 7) = 2(40 + 35 + 56) = 2 × 131 = 262 inch2.
How to Find the Surface Area of a Rectangular Prism?
The surface area of a rectangular prism can be calculated using the following steps:
- Step 1: Check if the given dimensions of the rectangular prism are in the same units or not. If not, convert them into the same units.
- Step 2: Once the dimensions are in the same units, understand the need to calculate the lateral surface area or the total surface area according to the given situation.
- Step 3: Implement the formula for lateral surface area 2h(l + b), or total surface area, 2 (lb + bh + lh).
- Step 4: Write the unit as square units along with the values thus obtained.
Now we know the formula and method to calculate the surface area of a rectangular prism, let us now understand how to calculate it with the help of an example.
Example: Determine the minimum area of the wrapping paper required to wrap a rectangular gift box with dimensions as given below:
- Length, l = 24 inches
- Breadth, b = 15 inches
- Height, h = 20 inches
Solution: In this case, we have to find the total surface area of the box. It can be calculated by following the steps given below:
Step 1: Determine the area of the top and bottom faces of the box.
The area of the bottom and the top surfaces are equal, therefore we can simply twice the area of the top or bottom of the box.
2lb = 2 × (24 × 15) = 2 × 360 = 720 inch2
Step 2: Next, we determine the area of the side faces of the box.
2bh = 2 × (15 × 20) = 2 × 300 = 600 inch2
2lh = 2 × (24 × 20) = 2 × 480 = 960 inch2
Step 3: Add the areas of all six faces to determine the total surface area of the box.
2(lb + bh + lh) = 2lb + 2bh + 2lh = 720 + 600 + 960 = 2280 inch2.
Important Notes on Surface Area of Rectangular Prism:
- A rectangular prism with all sides equal is called a cube.
- A rectangular prism in which the faces are not perpendicular to each other is called an oblique rectangular prism.
- If all the edges of a rectangular prism are equal, then the surface area of the prism will be equal to 6 times the area of each face.
- If all the edges of a rectangular prism are equal to 'l', then the volume of the prism is 'l3'.
from a handpicked teacher in LIVE 1-to-1 classes
Pentagonal Prism
In geometry, a pentagonal prism is a three-dimensional shape with two pentagonal bases and five rectangular faces. So, a pentagonal prism has a total of 7 faces, 15 edges, and 10 vertices out of which 2 faces are pentagonal in shape. We can find the volume and surface area of a pentagonal prism as we do for any other 3D shape. Let's learn everything about pentagonal prism in detail in this article.
What is a Pentagonal Prism?
A pentagonal prism is a three-dimensional solid that has two pentagonal bases - bottom and top. All the other sides of a pentagonal prism have the shape of a rectangle. It is easy to understand the shape of a pentagonal prism by drawing a pentagon on a piece of paper using straight lines. Then imagine it stretching up from the sheet of paper. The 3D shape so formed will be a pentagonal prism!

A pentagonal prism has:
- 7 faces
- 15 edges
- 10 vertices
- Pentagon bottom and top
Pentagonal Prism Examples
Here are some real-life examples of a pentagonal prism. Look at the figures given below and look around you to find more examples of pentagonal prism and make your own list.
- U.S. Defence Department Headquarter
- Barns and boxes
- Decorative items

Properties of a Pentagonal Prism
A pentagonal prism consists of various properties that are unique to this solid shape. Listed below are some of the properties of a pentagonal prism:
- A pentagonal prism has 15 edges, 7 faces, and 10 vertices.
- The base of a pentagonal prism is in the shape of a pentagon.
- The sides of a pentagonal prism are shaped like a rectangle.
- A pentagonal prism is a type of heptahedron, which is a polyhedron with seven plane faces.
- A pentagonal prism can also be called a five-sided polygon prism.
- The cross-section of a pentagonal prism is a pentagon.
Types of Pentagonal Prisms
Pentagonal prisms can be categorized into the following types:
- Regular pentagonal prisms
- Right pentagonal prisms
- Oblique pentagonal prisms
Regular Pentagonal Prisms
If all the sides of a pentagonal prism are equal in length, it is called a regular pentagonal prism. Note the following properties of a regular pentagonal prism.
- All rectangular faces of a regular pentagonal prism are congruent.
- When the pentagonal faces of a regular pentagonal prism are the bases, the rectangular faces of the prism are said to be lateral.
Right Pentagonal Prism
If the pentagon faces of a pentagonal prism are congruent and parallel, and the rectangular faces are perpendicular to the pentagon faces, it is called a right pentagonal prism.

Oblique Pentagonal Prism
If the pentagon faces of a pentagonal prism are not exactly on top of each other, that is, when the rectangular faces are not perpendicular to the pentagon faces, it's called an oblique pentagonal prism.

Pentagonal Prism Formulas
The formulas of a pentagonal prism help us to find out the surface area and its volume very quickly and easily. Observe the following figure where 'a' is the apothem length of the prism, 'b' is the base length, and 'h' is the height of the prism.
Surface Area of a Pentagonal Prism
The surface area of a pentagonal prism gives the area of each face of the prism. The formula for the surface area of a pentagonal prism is:
Surface Area = (5ab + 5bh) square units
Pentagonal Prism Volume
The volume of a pentagonal prism gives the capacity of the prism. The formula for the volume of a pentagonal prism is:
Volume = (5/2 × abh) cubic units
Example: If the apothem length 'a' of a pentagonal prism is 5 feet, the base length 'b' is 4 feet, and the height 'h' is 6 feet.

The surface area of the pentagonal prism is: 5ab + 5bh = (5 × 5 × 4) + (5 × 4 × 6) = 100 + 120 = 220 square feet.
The volume of the pentagonal prism is: 5/2 × abh = 5/2 × 5 × 4 × 6 = 300 cubic feet.
Net of a Pentagonal Prism
The net of a pentagonal prism is the flattened view of the shape. When the pentagonal prism is opened, the two shapes that can be seen are the rectangle and the pentagon. The net of the pentagonal prism consists of the two pentagons which is the base of the shape and rectangles which is the sides or faces of the shape.

Related Articles:
Check out these interesting articles on the pentagonal prism. Click to know more!
from a handpicked teacher in LIVE 1-to-1 classes
Volume of Triangular Prism
The volume of a triangular prism is the space occupied by it from all three dimensions. A prism is a solid object which has identical bases, flat rectangular side faces, and the same cross-section all along its length. There are different types of prisms that are classified and named as per the shape of their base. A triangular prism has 2 identical triangular bases and 3 rectangular lateral faces.
What is the Volume of a Triangular Prism?
The volume of a triangular prism can be calculated by taking the product of the area of the triangular base and the height of the prism which is also known as the length of the prism. For this, let us first understand what a triangular prism looks like.
Definition of Triangular Prism
A triangular prism is a polyhedron made up of two triangular bases and three rectangular sides. Or, it can be considered as a pentahedron (as it has 5 faces altogether) wherein the edges and vertices of the bases are joined with each other by three rectangular sides. By definition, the two triangular bases are parallel and congruent to each other. It has:
- 2 bases (which are congruent triangles)
- 3 side faces (which are congruent rectangles)
- Total number of faces - 5
- 9 edges
- 6 corners or vertices
The length of the triangular prism is the perpendicular distance between the centers of the two bases. It is represented by "l" in the figure given below.

Observe the triangular prism shown above where 'b' is the base of each side of two congruent triangles, 'h' is the height of the base triangle, and 'l' is the length of the prism.
Volume of Triangular Prism Formula
The volume of a triangular prism is the space inside it or the space occupied by it. It is measured in cubic units such as cm3, m3, in3, etc. We will see the formulas to calculate the volumes of different types of triangular prisms. The volume of any prism is obtained by multiplying its base area by its length.
The volume of a prism = base area × length of the prism
We will use this formula to calculate the volume of a triangular prism as well. We know that the base of a triangular prism is a triangle. By applying the above formula to a triangular prism, we get,
Volume of a triangular prism = area of base triangle × length of the prism
Here, we can find the area of the base triangle based on its type and the available information. The following list shows the formulas to find the area of the base triangle.
- If the base triangle is an equilateral triangle (in this case, the prism is called equilateral triangular prism) with each side 'a', then its area = √3a2/4
- If the triangle's base 'b' and height 'h' are given, then its area = (1/2) bh
- If the base triangle is a right-angled triangle (in this case, the prism is called a right triangular prism) with two legs 'b' and 'h' then its area = (1/2) bh
- If the base triangle is an isosceles triangle with its sides to be 'a', 'a', and 'b' then its area is (b/4) × √(4a2 - b2)
- If the base triangle is a scalene triangle where all three sides 'a', 'b', and 'c' are given, then its area is calculated using √[s(s-a)(s-b)(s-c)]; where, s = (a + b + c)/2. Note that you can apply this formula (which is also called Heron's formula) for an isosceles triangle (or) an equilateral triangle as well.
- If the base triangle's two sides 'a' and 'b' and the included angle 'θ' are given, then its area is found using 1/2 ab sin θ

How to Find the Volume of Triangular Prism?
The volume of a triangular prism can be calculated with the help of the following steps and the example given below. Before that make sure that all measurements are of the same units.
- Step 1: Identify the type of the base triangle and find its area using a suitable formula (as explained in the previous section).
- Step 2: Identify the length of the prism (Note that this length of the prism is also known as the height of the prism, and it should not be confused with the height of the base triangle).
- Step 3: Multiply the base area (from step 1) and the length of the prism to find the volume.
Example: Calculate the volume of the triangular prism whose length is 15 in and whose base is an equilateral triangle of side 6 inches.
Solution: The volume of the triangular prism can be calculated using the following steps.
- Step 1: The base triangle is an equilateral triangle with its side as a = 6. So its area is found using the formula, √3a2/4 = √3(6)2/4 = 9√3 square inches.
- Step 2: The length of the prism is 15 in.
- Step 3: The volume of the given triangular prism = base area × length = 9√3 × 15 = 135√3 cubic inches.
Tips on Volume of Triangular Prism
- The length of a triangular prism is also known as the height of the prism.
- This height of the prism should not be confused with the height of the base triangle.
Volume of Rectangular Prism
The volume of a rectangular prism is the measurement of the total space inside it. Imagine a rectangular container filled with water. In this case, the total quantity of water that the container can hold is its volume. A prism is a polyhedron having identical bases, flat rectangular side faces, and the same cross-section all along its length. Prisms are classified on the basis of the shape of their base. A rectangular prism is categorized as a three-dimensional shape. It has six faces and all the faces of the prism are rectangles. Let us learn the formula to find the volume of a rectangular prism in this article.
What is the Volume of Rectangular Prism?
The volume of a rectangular prism is defined as the space occupied within a rectangular prism. A rectangular prism is a polyhedron that has two pairs of congruent and parallel bases. It has 6 faces (all are rectangular),12 sides, and 8 vertices. As the rectangular prism is a three-dimensional shape (3D shape), the unit that is used to express the volume of the rectangular prism is cm3, m3 and so on. In mathematics, any polyhedron, having all such characteristics can be referred to as a Cuboid.
Volume of Rectangular Prism Formula
The formula for the volume of a rectangular prism = base area × height of the prism. Since the base of a rectangular prism is a rectangle, its area will be l × w. This area is then multiplied by the height of the prism to get the volume of the prism. Therefore, another way to express this formula is by multiplying the length, width, and height of the prism and write the value in cubic units (cm3, m3, in3, etc).
Therefore, the formula for the volume of a rectangular prism is, volume of a rectangular prism (V) = l × w × h, where
- “l” is the base length
- “w” is the base width
- “h” is the height of the prism

To find the volume of the rectangular prism, we multiply the length, width, and height, that is the area of the base is multiplied by the height. It should be noted that the volume is measured in cubic units.
There are two types of rectangular prisms - right rectangular prisms and oblique prisms.
- In the case of a right rectangular prism, the bases are perpendicular to the other faces.
- In the case of an oblique rectangular prism, the bases are not perpendicular to the other faces. Thus, the perpendicular drawn from the vertex of one base to the other base of the prism will be taken as its height.
It should be noted that we can apply the same formula to calculate the volume of the prism, that is the rectangular prism volume formula, v = lwh, irrespective of the type of rectangular prism.
How to Find the Volume of a Rectangular Prism?
Before calculating the volume of a rectangular prism using the formula, we need to make sure that all the dimensions are of the same units. The following steps are used to calculate the volume of a rectangular prism.
- Step 1: Identify the type of the base and find its area using a suitable formula (as explained in the previous section).
- Step 2: Identify the height of the prism, which is perpendicular from the top vertex to the base of the prism.
- Step 3: Multiply the base area and the height of the prism to get the volume of the rectangular prism in cubic units. Volume = base area × height of the prism
Example: Calculate the volume of a rectangular prism whose height is 8 in and whose base area is 90 square inches.
Solution: We can calculate the volume of the rectangular prism using the following steps:
- Step 1: The base area is already given as 90 square inches.
- Step 2: The height of the prism is 8 in.
- Step 3: The volume of the given rectangular prism = base area × height of the prism = 90 × 8 = 720 cubic inches.
from a handpicked teacher in LIVE 1-to-1 classes
Rectangular Prism
A rectangular prism is a three-dimensional shape, having six faces, where all the faces (top, bottom, and lateral faces) of the prism are rectangles such that all the pairs of the opposite faces are congruent. Like all three-dimensional shapes, a rectangular prism also has volume and surface area. A rectangular prism is also known as a cuboid. Let us learn more about a rectangular prism along with the formulas to find its volume and surface area.
What is a Rectangular Prism?
A rectangular prism is a prism whose bases (the top face and the bottom face) are also rectangles. It has 6 faces in all, out of which there are 3 pairs of identical opposite faces, i.e., all the opposite faces are identical in a rectangular prism. It has three dimensions, length, width, and height. Some examples of a rectangular prism in real life are rectangular tissue boxes, school notebooks, laptops, fish tanks, large structures such as cargo containers, rooms, storage sheds, etc. The following figure shows a rectangular prism and its net, which is a two-dimensional representation of the prism when its faces are opened on a 2D plane.

Faces Edges Vertices of a Rectangular Prism
A rectangular prism has 6 faces, 12 edges (sides) and 8 vertices (corners). In the 12 edges, 3 edges intersect to form right angles at each vertex.
Types of Rectangular Prisms
There are two types of rectangular prisms that are classified depending on the shape of the faces or the angle made by the faces with the base.
- Right rectangular prism: In a right rectangular prism, the faces are perpendicular to each of its bases. In this, all side faces are rectangles.
- Oblique rectangular prism: In an oblique rectangular prism, the faces are not perpendicular to the bases. In other words, the faces in this prism are parallelograms.
In general, a rectangular prism without any specifications is a right rectangular prism.

Properties of Rectangular Prism
The properties of a rectangular prism are given below which help us to identify it easily.
- A rectangular prism has 6 faces, 8 vertices, and 12 edges.
- In a right rectangular prism, the faces are rectangles, whereas, in an oblique rectangular prism, the faces are parallelograms.
- It has 3 dimensions which are length, width, and height.
- The opposite faces of a rectangular prism are congruent.
Rectangular Prism Formulas
In this section, we will learn the formulas of the volume and surface area of a rectangular prism. For both of these, let us consider a rectangular prism of length 'l', width 'w', and height 'h'. Along these dimensions, let us assume that 'l' and 'w' are the dimensions of the base. Here are the formulas for the volume and surface area of a rectangular prism.

Let us see how to derive these formulas.
Volume of Rectangular Prism
The volume of a rectangular prism is the space that is inside it. We know that the volume of any prism is obtained by multiplying its base area by its height. Here,
- The base area of the rectangular prism = lw (using the area of a rectangle formula)
- The height of the rectangular prism = h
Thus, the volume of the rectangular prism, V = lw × h = lwh.
Surface Area of Rectangular Prism
There are two types of surface areas of a rectangular prism, one is the total surface area (TSA) and the other is the lateral surface area (LSA).
- The total surface area of a rectangular prism is the sum of the areas of all of its faces.
- The lateral surface area of a rectangular prism is the sum of the areas of all its side faces (excluding the bases).
We can calculate the areas of the side faces of a rectangular prism using its net.
The total surface area (TSA) of a rectangular prism
= The sum of areas of all faces
= lw + lw + wh + wh + hl + hl
= 2 (lw + wh + hl)
The lateral surface area (LSA) of a rectangular prism
= The sum of areas of side faces
= wh + wh + hl + hl
= 2 (wh + hl)
We will see the applications of these volume and surface area formulas of a rectangular prism in the section of Rectangular Prism Examples given below.
☛ Related Links

Rectangular Prism Examples
Example 1: Joe has a chocolate box whose shape resembles a rectangular prism. Its length is 6 in, height is 2 in and width is 4 in. Find the volume of the box.
Solution:
The dimensions of the given chocolate box are,
length, l = 6 in
width, w = 4 in
height, h = 2 in
Its volume is, V = lwh
= 6 × 4 × 2
= 48 in3
Answer: The volume of the box = 48 in3.
Example 2: A gift is packed in a rectangular box (rectangular prism) of dimensions 15 in, 10 in, and 8 in and it needs to be wrapped with gift paper. How much gift paper is required to wrap the gift box?
Solution:
The dimensions of the given gift box are,
length, l = 15 in
width, w = 10 in
height, h = 8 in
To find the amount of gift paper required, we need to find the total surface area of the box.
TSA of a rectangular prism = 2 (lw + wh + hl)
= 2 [(15 × 10) + (10 × 8) + (8 × 15)]
= 2 (150 + 80 + 120)
= 700 in2.
Answer: The amount (area) of the gift paper required = 700 in2.
Practice Questions on Rectangular Prism
Q.1
Olivia's mother surprised her with pasta packed in a rectangular prism shaped lunch box. How much quantity of pasta is served to Olivia given that the dimensions of the rectangular prism are as follows:
length= 5 in , width= 4 in, height= 3 in
The volume of lunch box is in³Q.2
Jack's grandmother handed over her beautiful hand carved chest to him for storing his stuff, especially woollens. The chest being 3 ft long and 2 ft wide having a shape of that of a rectangular prism has a capacity of 12 cubic ft. Find its height.
The depth of the chest is ft.Q.3
Ms Jeniffer gives prizes to the students of her class for performing acts of kindness. She displays prizes like colorful pencils, fancy erasers and color pens in a glass case, shaped more of a rectangular prism of length = 16 in, width = 5 in and height = 3 in. Find the total surface area of the prize case.
The total surface area of prize case is in2
FAQs on Rectangular Prism
What is a Rectangular Prism?
A rectangular prism is a 3-d solid shape that has 6 rectangular faces in which all the pairs of opposite faces are congruent. It has 8 vertices, 6 faces, and 12 edges. A few real-life examples of a rectangular prism include rectangular fish tanks, shoe boxes, etc.
What is a Rectangular Prism also Known as?
A rectangular prism is also known as a cuboid. It resembles a cube, but it is not a cube. All its properties are the same as that of a cube except that its faces are rectangles, whereas the faces of a cube are squares.
What is the Difference Between a Cube and a Rectangular Prism (Cuboid)?
Both cube and cuboid are prisms. A cube has 6 faces which are identical squares whereas a rectangular prism has 6 faces in which all the faces are rectangles. The opposite faces in a rectangular prism are identical.
What is the Ratio of Corners to Faces in Rectangular Prisms?
A rectangular prism has 8 corners (vertices) and 6 faces. So the ratio of the corners to faces in a rectangular prism is 8 : 6 (or) 4 : 3.
Why is a Rectangular Prism Called a Polyhedron?
A polyhedron is a 3-d shape in which all the 6 faces are in the shape of a polygon, i.e., in a polyhedron, the top and bottom faces are congruent polygons and the remaining 4 faces are lateral faces that are parallelograms. Therefore, it is called a polyhedron.
What is the Volume of a Rectangular Prism?
The volume of a rectangular prism is the space inside the prism. It is calculated by multiplying its base area by its height. Thus, the formula for the volume of a rectangular prism is Volume (V) = lwh; where 'l' is the length, 'w' is the width, and 'h' is the height of the prism and its base area (area of the rectangle of length 'l' and width 'w') is lw.
What is the Total Surface Area of a Rectangular Prism?
The total surface area of a rectangular prism is obtained by adding the areas of all its faces. Thus, the total surface area (TSA) of a rectangular prism is TSA = 2 (lw + wh + hl); where 'l' is the length, 'w' is the width, and 'h' is the height of the prism.
What is the Lateral Surface Area of a Rectangular Prism?
The lateral surface area of a rectangular prism is the sum of the areas of all its faces excluding the bases. Thus, the lateral surface area (LSA) of a rectangular prism of length 'l', width 'w', and height 'h' is LSA = 2 (wh + hl).
What is the Net of a Rectangular Prism?
The net of a rectangular prism is a two-dimensional representation of the prism which shows the faces of the prism if they are laid out flat. The net of a triangular prism has 6 rectangles in which 2 rectangles are the bases and the other 4 rectangles are its lateral faces.
What is a Right Rectangular Prism?
A right rectangular prism is a three-dimensional (3D) solid shape which has 6 faces, 12 edges, and 8 vertices. It is commonly known as the cuboid. All the angles that are formed at the vertices of this prism are right angles.




Post a Comment
Post a Comment