प्रिज्म

प्रिज्म क्या है?

सभी तरफ से समतल फलकों से बनी ठोस आकृति को प्रिज्म कहते हैं। प्रिज्म में दो प्रकार की सतह होती हैं। ऊपर और नीचे के समान फलक आधार कहलाते हैं। किसी प्रिज्म के ऊपर और नीचे फलकों के अलावा अन्य फलकों को इसके पार्श्व फलक कहा जाता है । सभी पार्श्व फलक एक-दूसरे के समान और समांतर होते हैं।

What is a prism?

A solid shape made up of flat faces on all sides is called a prism. Prism has two types of surfaces. The identical faces at the top and bottom are called Bases. Apart from the top and bottom faces of a prism, other faces are called its lateral faces. All the lateral faces are equal and parallel to each other.

प्रिज्म के आधारों के आकार के आधार पर ही प्रिज्म का नाम रखा जाता है।  उदाहरण के लिए, यदि किसी प्रिज्म का आधार त्रिकोणीय है तो उसे त्रिकोणीय प्रिज्म कहा जाता है।

The name of the prism is kept on the basis of the shape of its bases. For example, if the base of a prism is triangular then it is called a triangular prism.

प्रिज्म के तत्व

प्रिज्म के तत्व प्रिज्म को चित्रित करने और समझने में मदद करते हैं।

किनारा: वह सीधी रेखा जो प्रिज्म के किन्हीं दो आसन्न शीर्षों को जोड़ती है, उसका किनारा कहलाती है। 

शीर्ष: प्रिज्म के वे कोने जहाँ किन्हीं दो किनारे मिलते हैं, शीर्ष कहलाते हैं। 

फलक: शीर्षों और किनारों से घिरी एक बंद, सपाट सतह को फलक सतह कहते हैं।

आधार : ऊपर और नीचे के समान फलक आधार कहलाते हैं।

पार्श्व फलक :- किसी प्रिज्म के ऊपर और नीचे फलकों से जुड़े अन्य फलकों को इसके पार्श्व फलक कहा जाता है । 

Elements Of Prism

The elements of a prism help to illustrate and understand prisms.

Edge: The straight line which joins any two adjacent vertices of a prism is called its edge.

Vertex: The corners of the prism where any two edges meet are called vertices.

Face: A closed, flat surface bounded by vertices and edges is called a face surface.

Base: The top and bottom equal faces are called base.

Lateral faces:- Other faces connected to the top and bottom of a prism are called its Lateral faces.

प्रिज्म के प्रकार 

किसी प्रिज्म के ऊपर और नीचे की समान सतहों (फलकों) को आधार कहते हैं। इन आधारों के आकृतियों के आधार पर ही किसी प्रिज्म का नाम रखा जाता है। 

1. त्रिकोणीय प्रिज्म : यदि किसी प्रिज्म का आधार त्रिकोणीय है तो उसे त्रिकोणीय प्रिज्म कहा जाता है। 

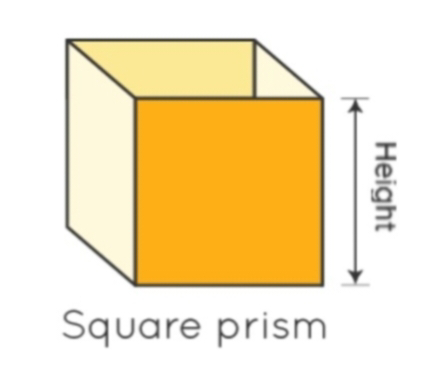
2. वर्गाकार प्रिज्म : वह प्रिज्म जिसका आधार एक वर्ग होता है। वर्गाकार प्रिज्म कहलाता है। वर्गाकार प्रिज्म को घन भी कहा जाता है।

3. आयताकार प्रिज्म : वह प्रिज्म जिसका आधार एक आयत होता है। आयताकार प्रिज्म कहलाता है। आयताकार प्रिज्म को घनाभ भी कहा जाता है।

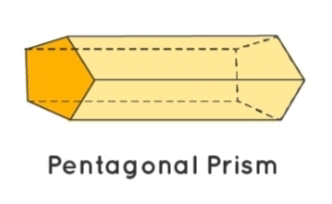
4. पंचभुजीय प्रिज्म : वह प्रिज्म जिसका आधार एक पंचभुजी होता है। पंचभुजीय प्रिज्म कहलाता है। पंचभुजीय प्रिज्म को पंचकोणीय प्रिज्म भी कहा जाता है। 

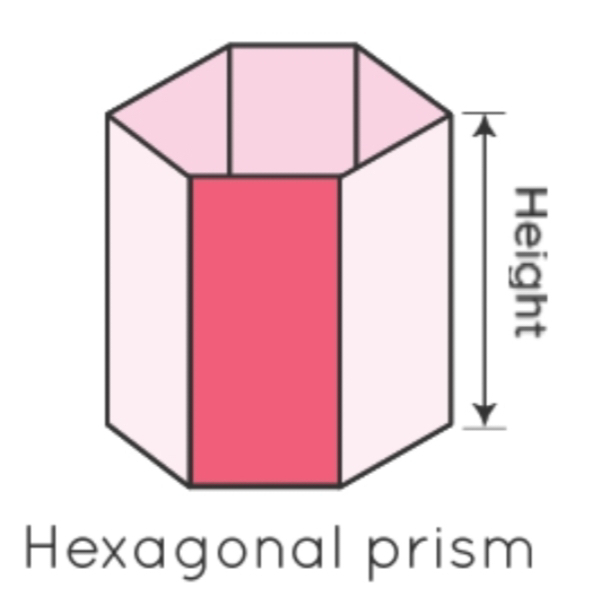
5. षटभुजीय प्रिज्म : वह प्रिज्म जिसका आधार एक षटभुज होता है। षटभुजीय प्रिज्म कहलाता है। षटभुजीय प्रिज्म को षटकोणीय प्रिज्म भी कहा जाता है। 

Types of prism

The identical surfaces (faces) at the top and bottom of a prism are called bases. The name of a prism is kept on the basis of the shapes of these bases.

1. Triangular Prism: If the base of a prism is triangular then it is called triangular prism.

2. Square prism: The prism whose base is a square. It is called a square prism. Square prism is also known as cube.

3.Rectangular Prism: The prism whose base is a rectangle is called rectangular prism. Rectangular prism is also called cuboid.

4. Pentagonal Prism: The prism whose base is a pentagon is called pentagonal prism. Pentagonal prism is also called pentangular prism.

5. Hexagonal Prism: The prism whose base is a hexagon is called hexagonal prism. Hexagonal prism is also called hexangular prism.

प्रिज्म का सतही क्षेत्रफल

किसी भी प्रिज्म के लिए, उसके सतह क्षेत्र की गणना निम्नलिखित सूत्र का उपयोग करके की जा सकती है:

सतह क्षेत्रफल = (2 ✕ आधार का क्षेत्र) + (आधार की परिधि ✕ ऊंचाई)

किसी प्रिज्म का सतही क्षेत्रफल उसके सभी आधारों और फलकों का कुल क्षेत्रफल होता है।

प्रिज्म का आयतन

किसी प्रिज्म के भीतर उपलब्ध स्थान को उस प्रिज्म का आयतन कहते हैं। प्रिज्म का आयतन भी घन इकाइयों में दर्शाया जा सकता है।

प्रिज्म का आयतन = आधार का क्षेत्रफल ✕ ऊँचाई

Surface Area of Prism

For any prism, its surface area can be calculated using the following formula:

Surface area = (2 ✕ area of base) + (circumference of base ✕ height)

The surface area of a prism is the total area of all its bases and faces.

Volume Of Prism

The space available inside a prism is called the volume of that prism. The volume of the prism can also be expressed in cubic units.

Volume of prism = area of base ✕ height

नियमित और अनियमित प्रिज्म

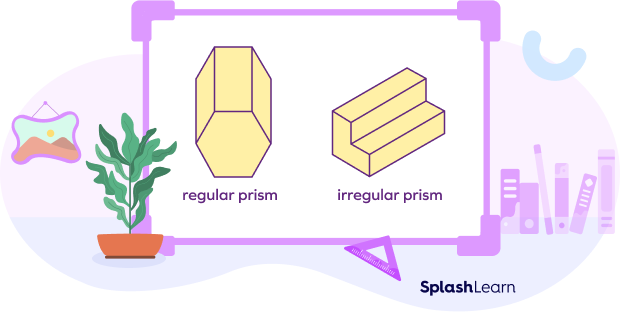
प्रिज्म के आधार के आकार का उपयोग उन्हें नियमित और अनियमित बहुभुजों में अलग करने के लिए किया जाता है। एक नियमित प्रिज्म एक नियमित बहुभुज वाला आधार होता है , जबकि एक प्रिज्म जिसका आधार एक अनियमित बहुभुज होता है उसे अनियमित प्रिज्म कहा जाता है।

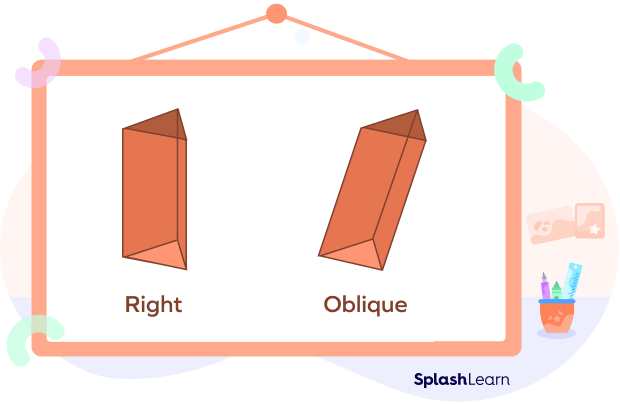
दायां प्रिज्म और ओब्लिक प्रिज्म

एक दाहिने प्रिज्म के दो सपाट सिरे होंगे और वे हर तरफ के चेहरे के साथ पूरी तरह से संरेखित होंगे। दूसरी ओर, एक तिरछा प्रिज्म दो आधारों के साथ कुछ झुका हुआ दिखाई देगा जो संरेखित नहीं हैं। ऐसे प्रिज्म के पार्श्व फलक समांतर चतुर्भुज होते हैं। 

चतुर्भुज के वर्ग से संबंधित हैं। इसका मतलब यह है कि पार्श्व फलक या तो समांतर चतुर्भुज, आयत या वर्ग भी हो सकते हैं क्योंकि उन सभी की विपरीत भुजाएँ एक दूसरे के समानांतर होती हैं। प्रिज्म का सबसे आम उदाहरण एक घनाकार है। इसका आधार आयताकार है और इसे आयताकार प्रिज्म कहा जाता है । 

प्रिज्म का आयतन

प्रिज्म के भीतर उपलब्ध स्थान प्रिज्म के आयतन को दर्शाता है। प्रिज्म के आयतन पर पहुंचने के लिए, हमें क्रॉस-सेक्शन के क्षेत्रफल का अनुमान लगाना होगा और फिर उन्हें प्रिज्म की गहराई से गुणा करना होगा। प्रिज्म का आयतन घन इकाइयों में दर्शाया जा सकता है।

प्रिज्म के आयतन की गणना करने का सूत्र इस प्रकार है:

आयतन = आधार का क्षेत्रफल ✕ ऊँचाई

प्रिज्म पर हल किये गये उदाहरण

(01) 1. 7 सेमी ऊंचाई और 60 सेमी² आधार क्षेत्रफल वाले प्रिज्म के आयतन की गणना करें।

हल : हम जानते हैं कि प्रिज्म का आयतन = आधार का क्षेत्रफल ✕ ऊँचाई

दिए गए प्रिज्म के लिए,

ऊँचाई = 7 सेमी और आधार का क्षेत्रफल = 60 सेमी²

इसलिए, दिए गए प्रिज्म का आयतन:

आयतन = 60 ✕ 7 = 420 सेमी³

उदाहरण 2. 25 सेमी² के आधार क्षेत्रफल, 24 सेमी की आधार परिधि और 10 सेमी की ऊंचाई वाले प्रिज्म के सतह क्षेत्र की गणना करें।

समाधान: हम जानते हैं कि एक प्रिज्म के लिए, 

सतह क्षेत्र = (2 ✕ आधार क्षेत्र) + (आधार परिधि ✕ ऊंचाई)

दिए गए प्रिज्म के लिए,

ऊंचाई = 10 सेमी और आधार का क्षेत्रफल = 25 सेमी² और आधार का परिमाप = 24 सेमी,

इसलिए, दिए गए प्रिज्म का सतह क्षेत्र:

सतह क्षेत्रफल = (2 ✕ 25) + (24 ✕ 10) = 50 + 240 = 290 सेमी²

उदाहरण 3. 25 सेमी² के आधार क्षेत्रफल और 12 सेमी की लंबाई वाले प्रिज्म का आयतन ज्ञात करें ।

समाधान : हम जानते हैं कि प्रिज्म का आयतन = आधार का क्षेत्रफल ✕ ऊँचाई

दिए गए प्रिज्म के लिए,

ऊँचाई = 12 सेमी और आधार का क्षेत्रफल = 25 सेमी²

इसलिए, दिए गए प्रिज्म का आयतन:

आयतन = 25 ✕ 12 = 300 सेमी³

प्रिज्म पर समस्याओं का अभ्यास करें

12.5 सेमी लंबाई वाले एक पंचकोणीय प्रिज्म के लिए, यदि आधार क्षेत्र 30 सेमी² है तो प्रिज्म का आयतन क्या होगा?

125 सेमी³

5 सेमी³

375 सेमी³

25 सेमी³

2

निम्नलिखित में से कौन सा प्रिज्म आकार का उदाहरण है?

घनक्षेत्र

कोन

गोला

सिलेंडर

3

यदि एक आयताकार प्रिज्म का आयतन 40 सेमी³ है और आधार का क्षेत्रफल 10 सेमी² है, तो प्रिज्म की ऊंचाई की गणना करें।

6 सेमी

4 सेमी

7 सेमी

10 सेमी

प्रिज्म पर अक्सर पूछे जाने वाले प्रश्न

एक प्रिज्म पिरामिड से किस प्रकार भिन्न है?

हालाँकि प्रिज्म और पिरामिड दोनों त्रि-आयामी हैं, एक प्रिज्म के दो समान आधार होते हैं जबकि पिरामिड का केवल एक ही आधार होता है।

क्या हम सिलेंडर को प्रिज्म मान सकते हैं?

चूँकि प्रिज्म एक बहुफलक है जिसके सभी फलक सपाट होते हैं, बेलन एक प्रिज्म नहीं है - इसकी सतह घुमावदार होती है ।

यदि किसी प्रिज्म के पार्श्व फलक आयताकार हों तो ऐसे प्रिज्म को क्या कहा जाता है?

इस स्थिति में, हम प्रिज्म को समकोण प्रिज्म कहेंगे।