Class 05 || Maths || Ch. 03 How Many Squares

Class 05 || Maths || Ch. 03 How Many Squares

Page: 34

Square:- Right Angled quadrilateral with equal side's.

Rectangul :- Right Angled quadrilateral with opposite equal side's

Perimeter: - Sum of all the sides along with boundary in units.

The perimeter of a square = 4 x (length of a side)

The perimeter of a rectangle = 2 x (length + breadth)
And, 

Area: - Total space covered along with boundary in square unit.

Area of a square = side x side 

                             ‌‌ = (side)²

Area of a rectangle = length x breadth

1.

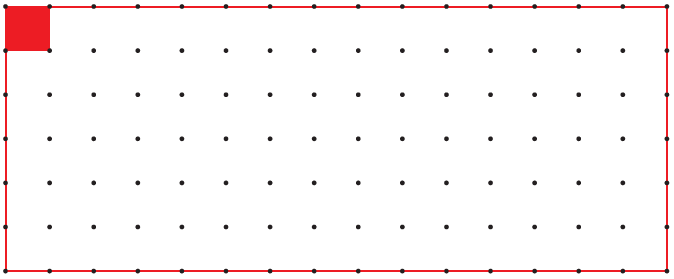
(i) Measure the side of the square on dotted sheet. Draw here as many rectangles as possible using 12 such squares.

Solution:-

The side of the square on dotted sheet is 1 cm.

(ii) How many rectangles could you make?

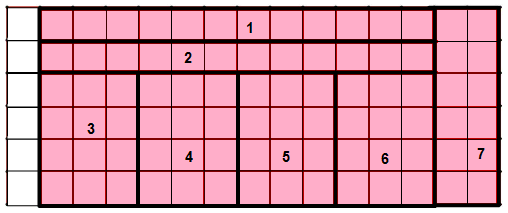
Sol. We can make 7 rectangle.

2. Each rectangle is made out of 12 equal squares, so all have the same area, but the length of the boundary will be different.

(i) Which of these rectangles has the longest perimeter?

Sol. From the above figure we can say that, rectangle 1 and 2 has the longest perimeter.

We know that, perimeter of rectangle= 2 (length + breadth)

= 2 (1 + 12)

= 2 × 13

= 26 cm

(ii) Which of these rectangles has the smallest perimeter?

Sol. From the above figure we can say that, rectangle 3, rectangle 4, rectangle 5 and 6 rectangle has the smallest perimeter.

We know that, perimeter of rectangle= 2 (length + breadth)

= 2 (3 + 5)

= 2 × 8

= 16 cm

3. Look at these interesting stamps.

(a) How many squares of one centimetre side does stamp A cover? ________

And stamp B? ________

Sol. 

Stamp A covers 18 squares of one centimeter side, and 

Stamp B covers 8 squares of one centimeter side.

(b) Which stamp has the biggest area?

Sol.

Stamp ‘A’ has biggest area, because it has 18 squares.

(i) How many squares of side 1 cm does this stamp cover?

Sol. This stamp has 18 squares of side 1 cm.

(ii) How much is the area of the biggest stamp.

Sol. The biggest stamp is in the shape of rectangle,

Length  = 6

Breadth = 3

The area of the biggest rectangle = Length × Breadth

= 3 × 6

= 18 cm²

c) Which two stamps have the same area?

Sol. Stamp ‘D’ and stamp ‘F’ have the same area.

(i) How much is the area of each of these stamps? ____ square cm.

Sol. 

For Stemp D

Length  = 4

Breadth = 3

We know that, area of rectangle = length × breadth

So, Area of stamp ‘D’ = 3 × 4

= 12 cm²

For Stemp F

Length  = 3

Breadth = 4

Area of stamp ‘F’ = 3 × 4

= 12 cm²

Therefore area of stamp ‘D’ is equal to area of stamp ‘F’.

d) The area of the smallest stamp is _____ square cm.

Sol. The smallest stamp is ‘E’.

Length  = 2

Breadth = 2

area of smallest stamp ‘E’ = length × breadth

= 2 × 2

= 4 cm²

The area of the smallest stamp is 4 square cm.

(i) The difference between the area of the smallest and the biggest stamp is _____ square cm.

Sol. In the figure is the biggest system is A and the smallest stemp is E.

and

Area of the biggest stamp = 18 cm²

Area of the smallest stamp = 4 cm²

Then,

The difference between the area of the smallest and the biggest stamp = 18 – 4

= 14 cm²

4. Guess

a) Which has the bigger area — one of your footprints or the page of this book?

Sol. When comparing the area of footprints and the area of page of this book, the area of page of this book is bigger than footprints.

b) Which has the smaller area—two five-rupee notes together or a hundred rupee note?

Sol. 

and 

A hundred rupee note has the smaller area.

c) Look at a 10 rupee-note. Is its area more than hundred square cm?

Sol. No, the area of 10 rupee note is not more than hundred square cm.

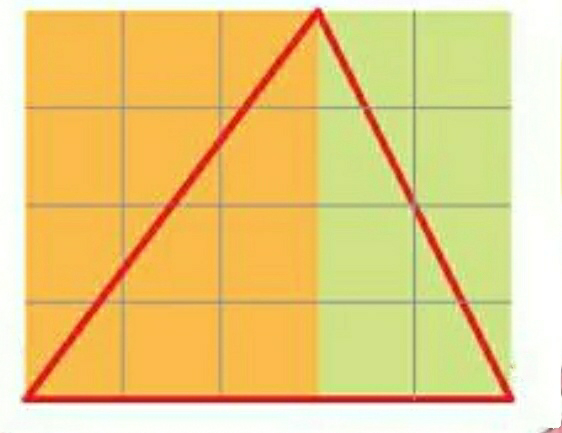
d) Is the area of the blue shape more than the area of the yellow shape? Why?

Sol. No, from the given image we can say that, the area of blue shape is equal to the area of yellow shape. Because, the yellow and blue shaped figures are divided into two triangles of equal areas.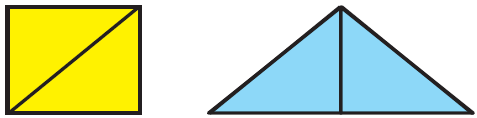

e) Is the perimeter of the yellow shape more than the perimeter of the blue shape? Why?

Sol. No, the perimeter of the yellow shape is less than the perimeter of the blue shape. With the help of a ruler, we can able find that the length of the boundary of the blue shape is more than the length of the boundary of the yellow shape.

Finding Areas Of Irregular Shape

★1 Trace the shape on a square paper 

★2 count the full squares and more than half squares 

★3 leave the less than half squares 

★4 Total number of the full square and more than half square is the area of irregular shape.

How Big is My Hand?

Trace your hand on the squared sheet on the next page.

How will you decide whose hand is bigger __________ your hand or your friend's hand?

What is the area of your hand? __________ square cm.

What is the area of your friend's hand? __________ square cm.

Sol. Do your self

Guess the area of

Sol.

Hen = about 3cm²

Dog = about 9cm²

5. Write the area (in square cm) of the shapes below.

Sol. 

(i) For area of shape A

Base = 3cm

Height = 4

Area of triangle fig A = ½ × base × height

= ½ × 3 × 4

= ½ × 12

= 6 cm²

(ii) For area of shape B

Counting

Complete squares    = 4 

Half (½) squares       = 8 

Quarter (¼) squares  = 4 

Area of square fig B = 4 complete square + 8 half squares + 4 quarter squares

= 4 + (½ × 8) + (¼ × 4)

= 4 + 4 + 1

= 9 cm²

(iii) For area of shape C

Counting

Complete squares    = 2 

Half (½) squares       = 4 

Area of fig C = 2 complete square + 4 half square

= 2 + (½ × 4)

= 2 + 2

= 4 cm²

(iii) For area of shape D

Counting

Complete squares    = 5 

Half (½) squares       = 2 

Area of fig D = 5 complete square + 2 half square

= 5 + (½ × 2)

= 5 + 1

= 6 cm²

(iii) For area of shape E

Counting

Complete squares    = 18 

Half (½) squares       = 6 

Area of fig E = 18 complete square + 6 half square

= 18 + (½ × 6)

= 18 + 3

= 21 cm²

(iii) For area of shape F

Counting

Complete squares    = 4 

Half (¾) squares       = 4 

Half (¼) squares       = 4 

Area of fig F = 4 complete square + 4 more than half + 4 quarter square

= 4 + (¾ × 4) + (¼ × 4)

= 4 + 3 + 1

= 8 cm²

6. The blue triangle is half of the big rectangle. Area of the big rectangle is 20 square cm. So the area of the blue triangle is _______ square cm.

Sol.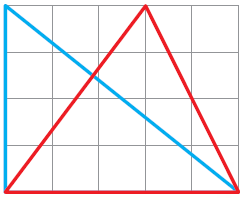 

From the question,

Area of the big rectangle is 20cm².

Area of the blue triangle is half of the big rectangle = 20/2

= 10 cm²

7. Ah, in it there are two halves of two different rectangles!

Now you find the area of the two rectangles Sadiq is talking about. What is the area of the red triangle? Explain.

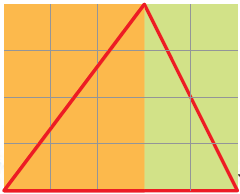
Sol. 

From the figure, we can say that,

The orange rectangle contains 12 squares

So, area of orange rectangle = 12 cm²

Now, area of the orange portion of triangle = 12/2 = 6cm²

Then, 

green rectangle contains 8 squares

So, the area of green rectangle = 8 cm²

Area of the yellow portion of triangle = 8/2 

= 4 cm²

Therefore, area of red triangle 

= 6 + 4

= 10 cm²

8. Suruchi drew two sides of a shape. She asked Asif to complete the shape with two more sides, so that its area is 10 square cm.

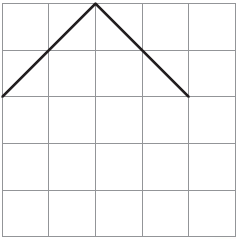He completed the shape like this.

(i) Is he correct? Discuss.

Sol. Yes, he is correct.

(ii) Explain how the green area is 4 square cm and the yellow area is 6 square cm.

Sol. 

For Green area

Green area contains = 2 complete square + 4 half square

= 2 + (½ × 4)

= 2 + 2

= 4 cm²

For Yellow area

Yellow area contains = 3 complete square + 2 more than half + 2 half filled

= 3 + 2 + (½ × 2)

= 3 + 2 + 1

= 6 cm²

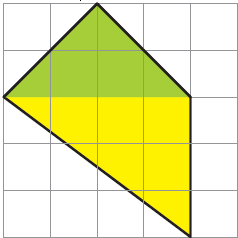
Oh, I thought of doing it differently! If you draw like this, the area is still 10 square cm.

(i) Is Suruchi correct? How much is the blue area? Explain.

For Yellow area

Yellow area contains = 4 complete square + 2 more than half + 8 half filled

= 4 + 2 + (½ × 8)

= 4 + 2 + 4

= 10 cm²

(ii) Can you think of some other ways of completing the shape? Try some other ways yourself.

Sol. 

We have read that the area of a triangle is half of area of a rectangle with same height and breadth.

Practice time

(1) This is one of the sides of a shape. Complete the shape so that its area is 4 square cm.

Sol. 

Completed shape contains = 2 complete square + 4 half square

= 2 + (½ × 4)

= 2 + 2

= 4 cm²

2. Two sides of a shape are drawn here. Complete the shape by drawing two more sides so that its area is less than 2 square cm.

Sol. 

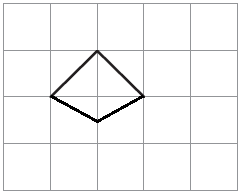
3. Here is a rectangle of area 20 square cm.

a) Draw one straight line in this rectangle to divide it into two equal triangles. 

What is the area of each of the triangles?

Sol. 

Area of rectangle = 10 × 2

= 20 cm²

Then, area of two equal triangles = 20/2

= 10 cm²

Because, it is given that straight line divides rectangle in to two equal triangles.

b) Draw one straight line in this rectangle to divide it into two equal rectangles. What is the area of each of the smaller rectangles?

Sol.

A line BC can be drawn as shown in this figure to divide the given rectangle ABEF into two equal rectangles ABCD & BCFE. 

Similarly, a horizontal line can also be drawn to divide the given rectangle into two equal rectangles.

 Area of big rectangle = 10 cm²

The area of each of the smaller rectangle = 20/2

= 10 cm²

c) Draw two straight lines in this rectangle to divide it into one rectangle and two equal triangles.

(i) What is the area of the rectangle?

Sol. Area of rectangle = length × breadth

= 2 × 5

= 10 cm²

(ii) What is the area of each of the triangles?

Sol. Area of each triangle = ½ × area of smaller rectangle

= ½ × 10

= 5 cm²

4. Puzzle with five squares

a) How many different shapes can you draw?

Sol. 

Using 5 squares, I can draw 12 shapes as show in the below,

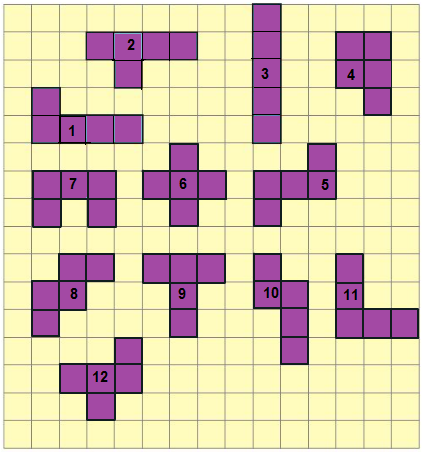
b) Which shape has the longest perimeter? How much?

Sol. Shape 4 has the smallest perimeter out of 12 shapes, rest of the shapes have same perimeter. i.e. = 1 + 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1 + 1 + 1 + 1 = 12 cm

c) Which shape has the shortest perimeter? How much?

Sol. Out of 12 shapes 4 has the smallest perimeter.

i.e. = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 10 cm.

d) What is the area of the shapes? _______ square cm. That’s simple!

Sol. There are 12 shapes each shapes has complete five squares. Area of 1 square is equal to 1 cm².

So, Area of each shape = 1 × 5 = 5 cm²

5. Ziri tried to make some other tiles. She started with a square of 2 cm side and made shapes like these.

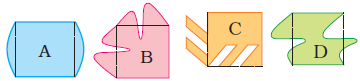Look at these carefully and find out:

(i) Which of these shapes will tile a floor (without any gaps)? Discuss. What is the area of these shapes?

Sol. By observing the given figure shape C and shape D will tile a floor without any gaps.

The shapes C and D will tile a floor without leaving any gaps. 

Design with shape C

Design with shape D

Area of each shape = 2 × 2 = 4 square cm²

For Practice (1)

01. Find the perimeter of the square whose side is 3 cm.

Sol. 01

Side of square = 3cm

perimeter of square = 4 × Side

                                p = 4 × 3

                                p = 12 cm

02. Find the perimeter of the square whose side is 10 cm.

03. Find the perimeter of the square whose side is 5 cm.

04. Find the perimeter of the square whose side is 7 cm.

05. Find the perimeter of the square whose side is 4 cm.

06. Find the Area of the square whose side is 10 cm.

Sol. 01

Side of square = 3cm

Area of square = Side × Side

                        A = 3 × 3

                         A = 9 cm²

07. Find the Area of the square whose side is 3 cm.

08. Find the Area of the square whose side is 10 cm.

09. Find the Area of the square whose side is 5 cm.

10. Find the Area of the square whose side is 7 cm.

11. Find the perimeter and area of the square whose side is 3 cm.

Sol. 01

(i) For Perimeter

Side of square = 3cm

perimeter of square = 4 × Side

                                p = 4 × 3

                                p = 12 cm

(ii) For Area

Side of square = 3cm

Area of square = Side × Side

                        A = 3 × 3

                         A = 9 cm²

12. Find the perimeter and area of the square whose side is 10 cm.

13. Find the perimeter and area of the square whose side is 5 cm.

14. Find the perimeter and area of the square whose side is 7 cm.

15. Find the perimeter and area of the square whose side is 4 cm.

For Practice (2)

01. Find the perimeter of the Rectangle whose sides are 3 cm and 4 cm.

Sol. 01

Length (l) of Rectangle = 3cm

Breadth (b) of Rectangle = 4cm

perimeter of Rectangle = 2 × l + 2× b

                                     p = 2 × 3 + 2 × 4

                                     p = 6 + 8 cm

                                     p = 14 cm

02. Find the perimeter of the Rectangle whose sides are 3 cm and 4 cm.

03. Find the perimeter of the Rectangle whose length and breadth are 3 cm and 4 cm.

04. Find the perimeter of the Rectangle whose length and breadth are 3 cm and 4 cm.

05. Find the perimeter of the Rectangle whose length and breadth are 3 cm and 4 cm.

06. Find the area of the Rectangle whose sides are 3 cm and 4 cm.

Sol. 06

Length (l) of Rectangle = 3cm

Breadth (b) of Rectangle = 4cm

Area of Rectangle =  l × b

                               A = 3 × 4

                               A = 12 cm²

07. Find the area of the Rectangle whose sides are 3 cm and 4 cm.

08. Find the area of the Rectangle whose length and breadth are 3 cm and 4 cm.

09. Find the area of the Rectangle whose length and breadth are 3 cm and 4 cm.

10. Find the area of the Rectangle whose length and breadth are 3 cm and 4 cm.

11. Find the perimeter and area of the Rectangle whose sides are 3 cm and 4 cm.

Sol. 01

(i) For Perimeter

Length (l) of Rectangle = 3cm

Breadth (b) of Rectangle = 4cm

perimeter of Rectangle = 2 × l + 2× b

                                     p = 2 × 3 + 2 × 4

                                     p = 6 + 8 cm

                                     p = 14 cm

(ii) For Area

Length (l) of Rectangle = 3cm

Breadth (b) of Rectangle = 4cm

Area of Rectangle =  l × b

                               A = 3 × 4

                               A = 12 cm²

12. Find the perimeter and area of the Rectangle whose sides are 3 cm and 4 cm.

13. Find the perimeter and area of the Rectangle whose length and breadth are 3 cm and 4 cm.

14. Find the perimeter and area of the Rectangle whose length and breadth are 3 cm and 4 cm.

15. Find the perimeter and area of the Rectangle whose length and breadth are 3 cm and 4 cm.