Ex 8.3
Ex 8.3
Question 1.
Evaluate:

Solution:
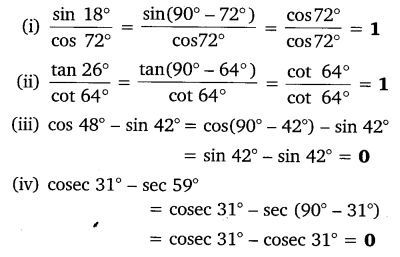
Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution:
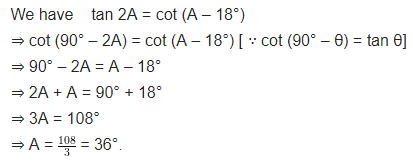
Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:
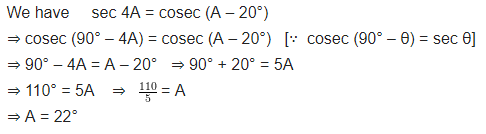
Question 6.
If A, B and C are interior angles of a triangle ABC, then show that: sin (B+C )/2 = cos A/2
Solution:
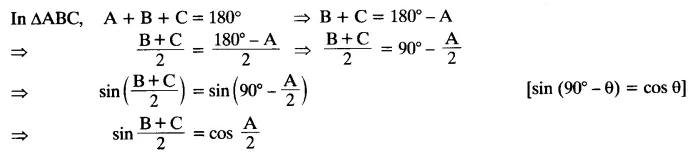
Question 7.
Express sin 61° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
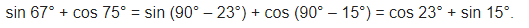
Question 1.
Evaluate:![]()
Solution: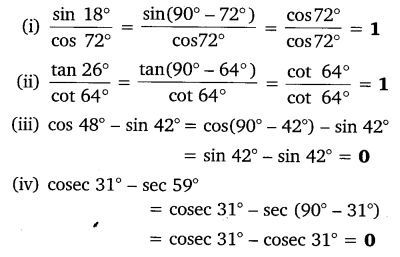
Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution: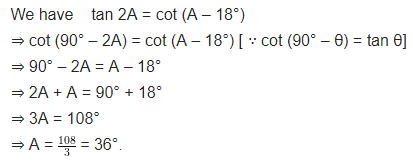
Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution: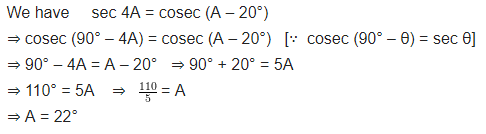
Question 6.
If A, B and C are interior angles of a triangle ABC, then show that: sin (
Solution: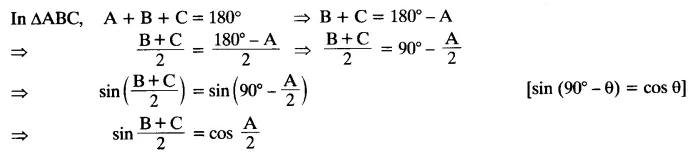
Question 7.
Express sin 61° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:![]()
Ex 8.4
Question 1.
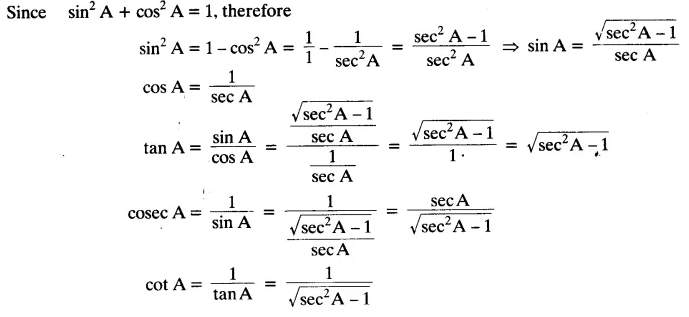
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.Solution:

Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
Question 3.Evaluate:
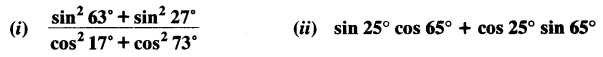
Solution:
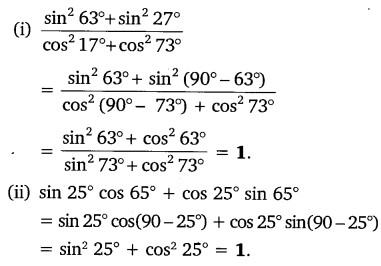
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A = ……
(A) 1 (B) 9
(C) 8 (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) = ………..
(A) 0 (B) 1
(C) 2 (D) -1
(iii) (sec A + tan A) (1 – sin A) = ………….
(A) sec A (B) sin A
(C) cosec A (D) cos A
(iv) 1+tan2A1+cot2A = ………..
(A) sec² A. (B) -1
(C) cot² A. (D) tan² A
Solution:

Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
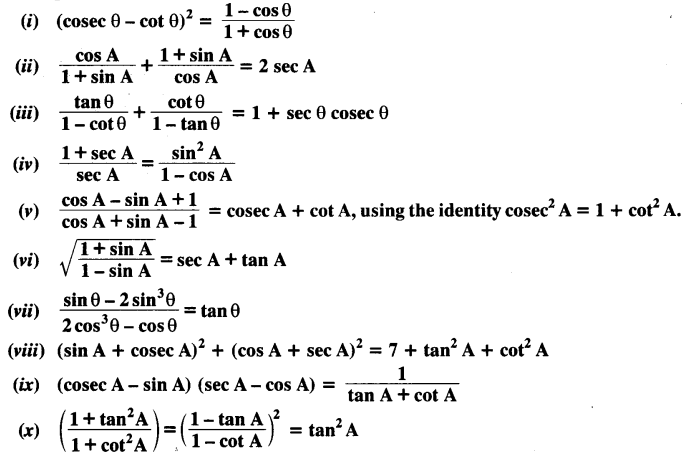
Solution:

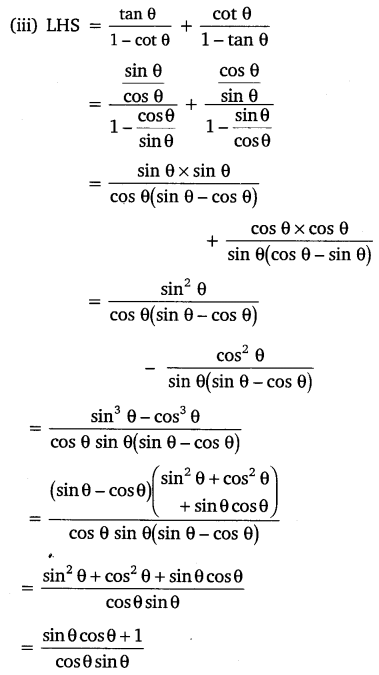

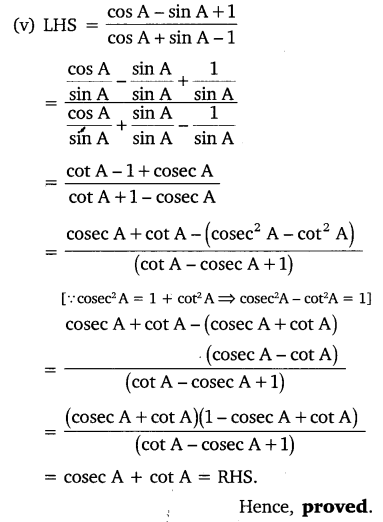


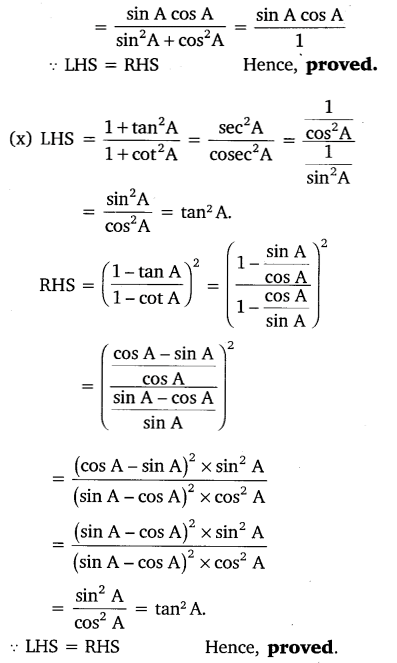
A
Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.Solution:

Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
Evaluate: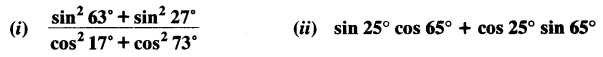
Solution: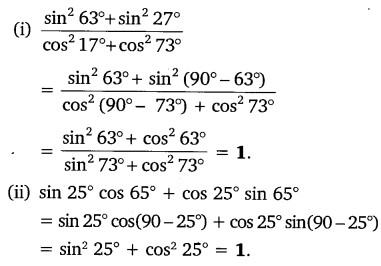
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A = ……
(A) 1 (B) 9
(C) 8 (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) = ………..
(A) 0 (B) 1
(C) 2 (D) -1
(iii) (sec A + tan A) (1 – sin A) = ………….
(A) sec A (B) sin A
(C) cosec A (D) cos A
(iv)
(A) sec² A. (B) -1
(C) cot² A. (D) tan² A
Solution:
Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.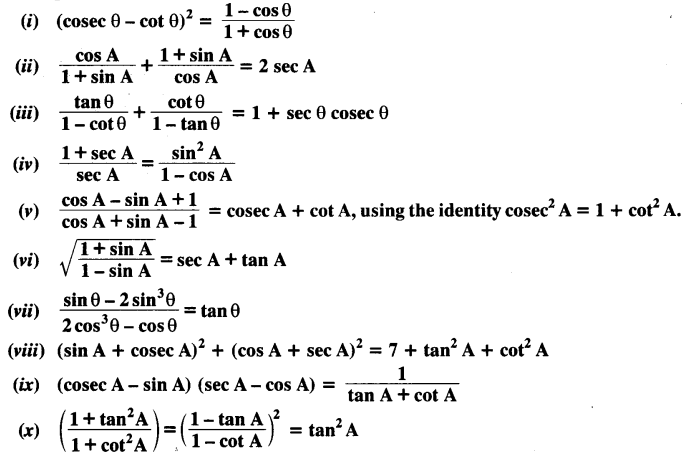
Solution:
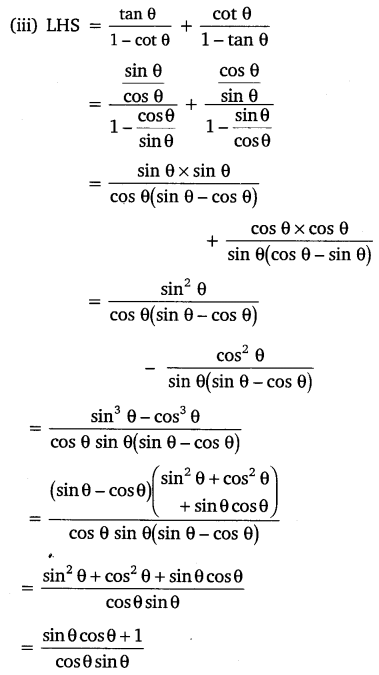

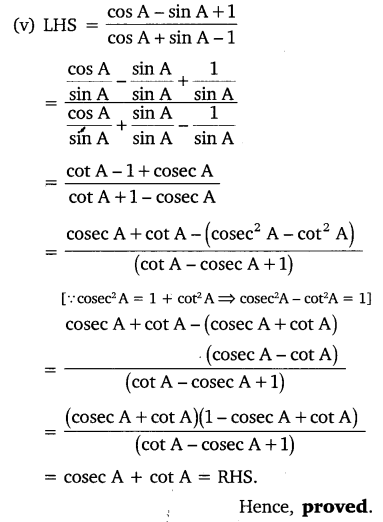



A


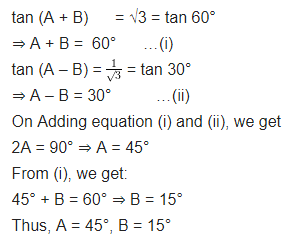
Post a Comment
Post a Comment