Exercise 6.3 Maths Class 10th

Triangles Class 10 Ex 6.3

Q. 1. State which pairs of triangles in the given figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :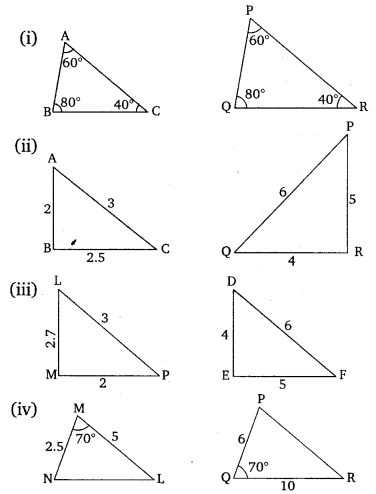

Solution:

Proofing:

As we know if in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.

This is referred as $AAA$ (Angle–Angle–Angle) criterion of similarity of two triangles.

Steps:

In $\Delta ABC$ and $\Delta PQR$

$$\begin{array}{c}\angle A=\angle P=60{}^{\circ }\end{array}$$

$$\begin{array}{c}\\ \angle B=\angle Q={80}^{\circ }\end{array}$$

$$\begin{array}{c}\\ \angle C=\angle R={40}^{\circ }\end{array}$$

All the corresponding angles of the triangles are equal.

By $AAA$ criterion $$\begin{array}{c}\Delta ABC\sim \Delta PQR\end{array}$$

As we know if in two triangles, side of one triangle are proportional to (i.e., in the same ratio ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar.

This is referred as $SS$ (Side–Side–Side) similarity criterion for two triangles.

Steps:

$In\Delta ABCand\Delta QRP$

$$\begin{array}{cc}\frac{A\mathrm{B/}}{QR}& =\frac{\mathrm{2/}}{4}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}BC/PR\; =\frac{\mathrm{2.5/}}{5}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}AC/PQ\; =\frac{\mathrm{3/}}{6}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}\\ \Rightarrow \frac{A\mathrm{B/QR}}{}& =\frac{B\mathrm{C/}}{PR}=\frac{A\mathrm{C/}}{PQ}=\frac{\mathrm{1/}}{2}\end{array}$$

All the corresponding sides of two triangle are in same proportion.

By $SS$ criterion $\Delta ABC\sim \Delta QPR$

As we know if in two triangles, side of one triangle are proportional to (i.e., in the same ratio ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar.

This is referred as $SSS$ (Side–Side–Side) similarity criterion for two triangles.

Steps:

In $\Delta LMP$ and  $\Delta FED$

$$\begin{array}{cc}\frac{L\mathrm{M/}}{FE}& =\frac{\mathrm{2.7/}}{5}\end{array}$$

$$\begin{array}{c}MP/ED\; =\frac{\mathrm{2/}}{4}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}LP/FD\; =\frac{\mathrm{3/}}{6}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ \Rightarrow \frac{L\mathrm{M/}}{FE}& \ne \frac{M\mathrm{P/ED}}{}=\frac{L\mathrm{P/}}{FD}\end{array}$$

All the corresponding sides of the two triangles are not in the same proportion.

Hence triangles are not similar.

$\Delta LMP\nsim \Delta FED$

(iv)

Proofing:

As we know if one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.

This criterion is referred to as the $SAS$ (Side–Angle–Side) similarity criterion for two triangles.

Steps:

In $\Delta NML$ and $\Delta PQR$

$$\begin{array}{cc}& \frac{N\mathrm{M/}}{PQ}=\frac{\mathrm{2.5/}}{5}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}ML/QR=\frac{\mathrm{5/}}{10}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \Rightarrow \frac{N\mathrm{M/PQ}}{}=\frac{M\mathrm{L/}}{QR}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \angle M=\angle Q={70}^{\circ }\end{array}$$

One angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional.

By $SAS$ criterion $\Rightarrow \Delta NML\sim \Delta PQR$  

(v)

Proofing:

As we know if one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.

This criterion is referred to as the $SAS$ (Side–Angle–Side) similarity criterion for two triangles.

Steps:

In $\Delta ABC$and $\Delta DFE$

$$\begin{array}{cc}& \frac{A\mathrm{B/}}{DF}=\frac{\mathrm{2.5/}}{5}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}BC/EF=\frac{\mathrm{3/}}{6}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}AB/DF=\frac{B\mathrm{C/}}{EF}=\frac{\mathrm{1/}}{2}\end{array}$$

$$\angle A=\angle F={\mathrm{80°}}^{}$$

But $\angle B$ must be equal to 

 The sides $AB,BC$ includes $\angle B$, not $\angle \mathrm{A.}$

Therefore, $SAS$ criterion is not satisfied

Hence,the triangles are not similar, $\Delta ABC\nsim \Delta DFE$

(vi)

As we are ware if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.

This may be referred to as the $AA$  criterion for two triangles.

Steps:

In $\Delta DEF$

$$\angle D={\mathrm{70°}}^{};\angle E={\mathrm{80°}}^{}$$

$\Rightarrow \angle F={\mathrm{30°}}^{}$

$[\because$ Sum of the angles in a triangle is ${\mathrm{180°}}^{}]$

Now ,In $\Delta DEFand\Delta PQR$

$$\begin{array}{cc}\angle E& =\angle Q={\mathrm{80°}}^{}\\ \angle F& =\angle R={\mathrm{30°}}^{}\end{array}$$

Pair of corresponding angles of the triangles are equal.

By $AA$ criterion $\Delta DEF\sim \Delta PQR$

Q. 2. In the given figure, ∆ODC ~ ∆OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.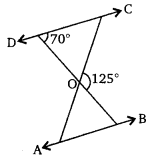

Solution:

Given:

∠COB=125°

∠CDO= 70°

In the given figure.

$$\begin{array}{c}\angle DOC={\mathrm{180°}}^{}-\angle COB\end{array}$$

$$\begin{array}{c}\angle DOC={\mathrm{180°}}^{}-{\mathrm{125°}}^{}\end{array}$$

$$\begin{array}{c}\\ & \angle DOC={\mathrm{55°}}^{}\end{array}$$

In $\Delta ODC$

$$\begin{array}{cc}\angle DC\mathrm{O\; +\; \angle DOC\; +\; \angle ODC}& ={\mathrm{180°}}^{}\end{array}$$

$$\begin{array}{c}[by\text{angle sum property}]\end{array}$$

$$\begin{array}{c}\\ & \\ \angle DCO& ={\mathrm{180°}}^{}-({\mathrm{55°}}^{}+{\mathrm{70°}}^{})\end{array}$$

$$\begin{array}{c}\\ \angle DCO& ={\mathrm{55°}}^{}\end{array}$$

In $\Delta ODC$ and $\Delta OBA$ 

$$\begin{array}{cc}& \Delta ODC\sim \Delta OBA\end{array}$$

$$\begin{array}{c}\\ & \Rightarrow \angle DCO=\angle OAB\end{array}$$

$$\begin{array}{c}\\ & \angle DCO={\mathrm{55°}}^{}\end{array}$$

Q. 3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OA/OC=OB/OD∙
Solution:

Given:  A trapezium ABCD in which diagonals AC and BD intersect at O.

AD||BC

To Prove: 

OA/OC = OB/OD

Proof: 

In $\Delta AOB,\Delta COD$

$$\begin{array}{cc}& \angle AOB=\angle COD\\ & \text{(V.O.A.}\text{)}\end{array}$$

$$\begin{array}{c}\\ & \\ & \angle BAO=\angle DCO\\ (A.I.A.)\end{array}$$

$$\begin{array}{c}\\ & \\ & \Rightarrow \Delta AOB\sim \Delta CO\mathrm{D.}\\ \left(\text{AA criterion}\right)\end{array}$$

Hence $\begin{array}{c}\frac{O\mathrm{A/}}{OC}=\frac{O\mathrm{B/}}{OD}\end{array}$

$\begin{array}{c}\frac{\mathrm{(V.O.A.\; =\; Vertically\; opposite\; angles)(A.I.A\; =\; Alternate interior\; angles )}}{}\end{array}$

Second Method

Given:  A trapezium ABCD in which diagonals AC and BD intersect at O.

AD||BC

To Prove: 

OA/OC = OB/OD

Construction :

OE||AB||CD

Proof: 

In $\Delta \mathrm{AD}B,$

$\mathrm{OE||AB}$

$\mathrm{AE/ED=OB/OD\; .......(1)}$

In $\Delta \mathrm{AD}B,$

$$\begin{array}{cc}& \mathrm{crown\; equation\; (1)\; and\; (2)}\end{array}$$

Hence $\begin{array}{c}\frac{O\mathrm{A/}}{OC}=\frac{O\mathrm{B/}}{OD}\end{array}$

Q. 4. In the given figure, 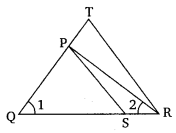QR/QS = QT/PR and ∠1 = ∠2. show that ∆PQR ~ ∆TQR.

Solution:

In $△PQR$

$$\begin{array}{cc}\angle 1& =\angle 2\end{array}$$

$$\begin{array}{c}\\ \Rightarrow PR& =PQ\end{array}$$

(sides opposite to equal angles are equal)

In $\Delta PQR$ and $\Delta TQR$

$$\begin{array}{cc}& \angle PQS=\angle TQR=\angle 1\\ \left(\text{Same angle}\right)\end{array}$$

$$\begin{array}{c}\\ & \\ & \frac{Q\mathrm{R/}}{QS}=\frac{Q\mathrm{T/}}{PQ}(\because PR=PQ)\end{array}$$

$$\begin{array}{c}\\ & \Rightarrow \Delta PQR\mathrm{~\Delta }TQ\mathrm{R.}\\ (\because \text{SAS criterion})\end{array}$$

Q 5. S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ ~ ∆RTS.
Solution:

In $\Delta RP\mathrm{Q\; and}\Delta RTS$

$$\begin{array}{cc}& \angle RPQ=\angle RTS\left(\text{Given}\right)\end{array}$$

$$\begin{array}{c}\\ & \angle PRQ=\angle TRS\\ \left(\text{Common Angle}\right)\end{array}$$

$$\begin{array}{c}\\ & \\ & \Rightarrow \Delta RPQ\mathrm{~\Delta }RT\mathrm{S.}\\ (\because \text{AA Criterion})\end{array}$$

Q 6. In the given figure, if ∆ABE ≅ ∆ACD, show that ∆ADE ~ ∆ABC.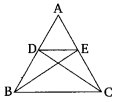

Solution:

In $\Delta ABEand\Delta ACD$

$$\begin{array}{cc}& \mathrm{\Delta ABE\; \cong \; \Delta ACD \; \; \; (Given)]}\end{array}$$

$$\begin{array}{cc}AE\; =AD& \\ [by\; CPCT].....& \left(1\right)\end{array}$$

$$\begin{array}{cc}& \\ & & \\ & AB=AC\end{array}$$

Now In $\Delta ADE,\Delta AB\mathrm{C\; ,}$

AD/AB = AE/ AC. …from (1) & (2)

and

∠DAF = ∠BAC (Common angle)

⇒ΔADE∼ ΔABC (SAS criterion)

Q. 7. In the given figure, altitudes AD and CE of ∆ABC intersect each other at the point P. Show that:
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC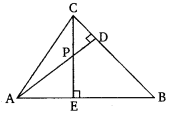

Solution:

(i)

Given: 

AD and CE are altitudes of ΔABC

To Prove:

ΔAEP  ∼ ΔCDP

Proof:

In $\Delta AEP$ and $\Delta CDP$

$$\begin{array}{cc}& \angle AEP=\angle CDP={90}^{\circ }\end{array}$$

$$\begin{array}{c}\\ & \left[\begin{array}{c}\therefore CE\perp A\mathrm{B\; and}AD\perp BC;altitudes\end{array}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ & \angle APE=\angle CP\mathrm{D.}\\ [V.O.A.]\end{array}$$

$$\begin{array}{c}\\ & \\ & \Rightarrow \Delta AEP\sim \Delta CPD\\ & \left[\text{AA Criterion}\right]\end{array}$$

In $\Delta ABDand\Delta CBE$

$$\begin{array}{cc}\angle ADB& =\angle CEB={90}^{\circ }\end{array}$$

$$\begin{array}{c}\\ \angle ABD& =\angle CBE\\ & \left[\text{Common angle}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow \Delta ABD& \sim \Delta CBE\\ [AA& \text{Criterion}]\end{array}$$

In $\Delta AEP$ and $\Delta ADB$

$$\begin{array}{cc}\angle AEP& =\angle ADB={90}^{\circ }\end{array}$$

$$\begin{array}{c}\\ \angle PAE& =\angle BAD\\ \left[\text{Common Angle}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow \Delta AEP& \sim \Delta AD\mathrm{B \; [AA\; Criterion]}\end{array}$$

$$\Delta PDCand\Delta BEC$$

Q. 8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE ~ ∆CFB.
Solution:

In a parallelogram ABCD

and in ΔABE, ΔCFB

∠BAE = ∠FCB 

(opposite angles of a 

 ∠AEB = ∠FBC 

[∵AE||BC and EB is a transversal alternate angle]

 ⇒ΔABE∼ΔCFE       (AA Criterion)

Q. 9. In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:

(i) $\begin{array}{c}\Delta ABC\sim \Delta AMP\end{array}$

(ii) $\begin{array}{c}\frac{C\mathrm{A/}}{PA}=\frac{B\mathrm{C/}}{MP}\end{array}$

Solution:

(i) In $\Delta ABC$ and $\Delta AMP$ 

$$\begin{array}{cc}& \angle ABC=\angle AMP={90}^{{}^{\circ }}\end{array}$$

$$\begin{array}{c}\\ & \angle BAC=\angle MAP\\ \left(\text{Common angle}\right)\end{array}$$

$$\begin{array}{c}\\ & \\ & \Delta ABC\sim \Delta AM\mathrm{P \; \; (AA\; Criterion)}\end{array}$$

In $\Delta AB\mathrm{C\; and\; \Delta AMP}$    

$\Delta \mathrm{ABC}$∼ΔAMP

$$\begin{array}{cc}\frac{C\mathrm{A/}}{PA}& =\frac{B\mathrm{C/}}{MP}\end{array}$$

Ex 6.3 Class 10 Maths Question 10.
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that:

(i)$\begin{array}{c}\frac{C\mathrm{D/}}{GH}=\frac{A\mathrm{C/}}{FG}\end{array}$

(ii)$\begin{array}{c}\Delta DCB\sim \Delta HGE\end{array}$

(iii) $\begin{array}{c}\Delta DCA\sim \Delta HGF\end{array}$

Solution:

(i)

Proofing:

In ΔABC  and ΔFEG 

$\angle C=\angle G$

$\begin{array}{c}\Rightarrow \frac{\angle C/}{2}=\frac{\angle G/}{2}\end{array}$

$\Rightarrow \angle ACD=\angle FGH$

($CD$ and $GH$ are bisectors of $\angle Cand\angle G$ respectively)

In $\Delta ADC$ and $\Delta FHG$

$$\begin{array}{cc}& \angle DAC=\angle HFG\\ & [\because \Delta ADC\sim \Delta FEG]\end{array}$$

$$\begin{array}{c}\\ & \\ & \angle ACD=\angle FGH\end{array}$$

$$\begin{array}{c}\\ \Rightarrow & \Delta ADC\sim \Delta FHG\\ \text{(AA Criterion)}\end{array}$$

If two triangles are similar, then their corresponding sides are in the same ratio.

$$\begin{array}{c}\Rightarrow \frac{C\mathrm{D/GH}}{}=\frac{A\mathrm{C/}}{FG}\end{array}$$

(ii) Proofing:

In $\Delta DCB$ and $\Delta HGE$

$$\begin{array}{cc}& \angle DBC=\angle HEG\\ [\because \Delta ABC\sim \Delta FEG]\end{array}$$

$$\begin{array}{c}\\ & \\ & \angle DCB=\angle HGE\\ [\because \frac{\angle AC\mathrm{B/}}{2}=\frac{\angle FG\mathrm{E/}}{2}]\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow & \Delta DCB\sim \Delta EH\mathrm{G.}\\ \text{(AA Criterion})\end{array}$$

In $\Delta DCA,\Delta HGF$

$$\begin{array}{cc}& \angle DAC=\angle HFG\\ [\because \Delta ABC\sim \Delta FEG]\end{array}$$

$$\begin{array}{c}\\ & \\ & \angle ACD=\angle FGH\\ [\because \frac{\angle AC\mathrm{B/}}{2}=\frac{\angle FG\mathrm{E/}}{2}]\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow & \Delta DCA\sim \Delta HGF\\ \text{(AA Criterion})\end{array}$$

Q. 11. In the given figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ∆ABD ~ ∆ECF.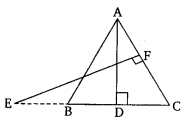

Solution:

Given: ΔABC is isosceles Δ in which AB=AC

⇒∠ABC=∠ACB (angle opposite to equal sides are equal)

In $\Delta ABD,\Delta ECF$

$$\begin{array}{cc}& \angle ADB=\angle EFC={90}^{\circ }\end{array}$$

$$\begin{array}{c}\\ & (\because AD\perp BC\text{and}EF\perp AC)\end{array}$$

$$\begin{array}{c}\\ & \angle ABD=\angle ECF\end{array}$$

$$\begin{array}{c}\\ & \Rightarrow \Delta ABD\sim \Delta ECF\\ & \left(\text{AA}\text{criterion}\right)\end{array}$$

Q. 12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆PQR (see in given figure). Show that ∆ABC ~ ∆PQR.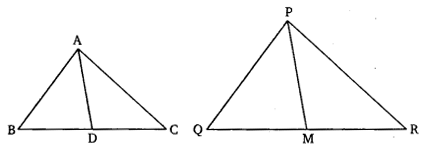

Solution:

Proofing:

In $\Delta ABC$ and $\Delta PQR$ 

$$\begin{array}{c}\frac{A\mathrm{B/}}{PQ}=\frac{B\mathrm{C/}}{QM}=\frac{A\mathrm{D/}}{PM}\text{[Given}\end{array}$$]

 AD  and PM are median of $\Delta ABC$ and $\Delta PQR$ respectively

$\begin{array}{cc}& \Rightarrow \frac{B\mathrm{D/QM}}{}=[\frac{\frac{B\mathrm{C/}}{\mathrm{2]/[QR/2]}}}{}=\frac{B\mathrm{C/}}{QR}\end{array}$

Now In $\Delta ABD\text{and}\Delta PQM$ 

$$\begin{array}{cc}& \frac{A\mathrm{B/}}{PQ}=\frac{B\mathrm{D/}}{QM}=\frac{A\mathrm{D/}}{PM}\end{array}$$

$$\Rightarrow \Delta ABD\sim \Delta PQM$$

Now in $\Delta ABC\text{and}\Delta PQR$

$$\begin{array}{cc}& \frac{A\mathrm{B/}}{PQ}=\frac{B\mathrm{C/}}{QR}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \left(\text{Given in the statement}\right)\end{array}$$

$$\begin{array}{c}\\ & \angle ABC=\angle PQR\\ [\because \Delta ABD\sim \Delta PQM]\end{array}$$

$$\begin{array}{c}\\ \Rightarrow \Delta ABC& \sim \Delta PQR\left[\text{SAS}\text{Criterion}\right]\end{array}$$

Q.13. D is a point on the side BC of a triangle ABC, such that ∠ADC = ∠BAC. Show that CA² = CB.CD.
Solution:

In ΔABC and ΔDAC

∠BAC = ∠ADC  

               (Given in the statement)

∠ACB=∠ACD   (Common angles)

⇒ΔABC∼ΔDAC  (AA criterion)

If two triangles are similar,then their corresponding sides are proportional

⇒CA/CD=CB/CA

⇒CA²=CB⋅CD

Q. 14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆PQR.
Solution:

Produce $AD$  to $E$ so that $AD=DE.$Join $CE$ Similarly, produce $PM$ to $N$ such that $PM=MN$, and Join $RN$.

In $\Delta ABD$  and $\Delta CDE$

$$\begin{array}{cc}& AD=DE\\ \text{[By}& \text{Construction]}\end{array}$$

$$\begin{array}{c}\\ & \\ & BD=DC\\ [\text{AP}& \text{is the median}]\end{array}$$

$$\begin{array}{c}\\ & \\ & \angle ADB=\angle CDE\\ [V.O.A& ]\end{array}$$

$$\begin{array}{c}\\ & \\ \therefore & \Delta ABD\cong \Delta CDE\\ [\text{By SAS}& \text{congruence}]\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow & AB=CE\left[CPCT\right]\dots \text{(i)}\end{array}$$

Also, in $\Delta PQM$ and $\Delta MNR$

$$\begin{array}{cc}PM& =MN\\ \text{[By}& \text{Construction]}\end{array}$$

$$\begin{array}{c}\\ & \\ QM& =MR\\ \text{[PM is}& \text{the median]}\end{array}$$

$$\begin{array}{c}\\ & \\ \angle PMQ& =\angle NM\mathrm{R.}\\ \text{[V.O.A}& \text{]}\end{array}$$

$$\begin{array}{c}\\ & \\ \therefore \Delta PQM& =\Delta MN\mathrm{R\; [By}\\ \text{SAS congruence}& \text{]}\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow PQ& =RN\left[CPCT\right]\text{... (ii)}\end{array}$$

Now,

$$\begin{array}{cc}& \frac{A\mathrm{B/}}{PQ}=\frac{A\mathrm{C/}}{PR}=\frac{A\mathrm{D/}}{PM}\left[Given\right]\end{array}$$

$$\begin{array}{c}\\ & \Rightarrow \frac{C\mathrm{E/RN}}{}=\frac{A\mathrm{C/}}{PR}=\frac{A\mathrm{D/}}{PM}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \left[\text{From (i)}\text{and (ii)}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ & \Rightarrow \frac{C\mathrm{E/RN}}{}=\frac{A\mathrm{C/}}{PR}=\frac{2A\mathrm{D/}}{2PM}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \Rightarrow \frac{C\mathrm{E/RN}}{}=\frac{A\mathrm{C/}}{PR}=\frac{A\mathrm{E/}}{PN}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & [2AD=AE\text{and}2PM=PN]\end{array}$$

$$\begin{array}{c}\\ & \\ & \therefore \Delta ACE\sim \Delta PRN\end{array}$$

$$\begin{array}{c}\\ & \left[\text{By SSS}\text{Similarity}\text{Criterion}\right]\end{array}$$

Therefore,

$$\angle CAE=\angle RPN$$

Similarly,

$$\angle BAE=\angle QPN$$

Therefore,

$$\begin{array}{cc}\angle CAE+\angle BAE& =\angle RPN+\angle QPN\end{array}$$

$$\begin{array}{c}\\ \Rightarrow \angle BAC& =\angle QPR\end{array}$$

$$\begin{array}{c}\\ \Rightarrow \angle A& =\angle P....\left(iii\right)\end{array}$$

Now, in $\Delta ABC\text{and}\Delta PQR$

$$\begin{array}{cc}& \frac{A\mathrm{B/}}{PQ}=\frac{A\mathrm{C/}}{PR}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \angle A=\angle P\dots \left[from\left(iii\right)\right]\end{array}$$

$$\begin{array}{c}\\ & \\ & \therefore \Delta ABC\sim \Delta PQR\end{array}$$

$$\begin{array}{c}\\ & \left[\text{By SAS}\text{similarity}\text{criterion}\right]\end{array}$$

Q. 15. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

Solution:

$AB$ is the pole $=$6 $m$

$BC$ is the shadow of pole $=$4 $m$

$PQ$ is the tower $=?$

$QR$ is the shadow of the tower $=$28 $m$

In $\Delta ABD$ and $\Delta PQR$

$$\begin{array}{cc}& \angle ABC=\angle PQR={90}^{\circ }\end{array}$$

$$\begin{array}{c}\\ & \left[\begin{array}{c}\text{The objects and shadow are}\\ \text{perpendicular to each other}\end{array}\right]\end{array}$$

$$\begin{array}{rl}& \mathrm{\angle }BAC=\mathrm{\angle }QP\mathrm{R }\end{array}$$

$$\begin{array}{c}\Rightarrow \Delta ABC\sim \Delta PQR\\ \text{(AA Criterion)}\end{array}$$

The ratio of any two corresponding sides in two equiangular triangles is always the same.

$$\begin{array}{cc}\Rightarrow \frac{A\mathrm{B/BC}}{}& =\frac{P\mathrm{Q/}}{QR}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ \frac{6\mathrm{m/}}{6m}& =\frac{P\mathrm{Q/}}{28m}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ \Rightarrow PQ& =\; (\frac{6\times \mathrm{28)/}}{4}m\end{array}$$

$$\begin{array}{c}PQ\; =42m\end{array}$$

Q.16. If AD and PM are medians of triangles ABC and PQR respectively, where ∆ABC ~ ∆PQR. Prove that AB/PQ=AD/PM∙

Solution:

Proofing:

$$\begin{array}{cc}& \Delta ABC\sim \Delta PQR\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow & \angle ABC=\angle PQR\\ & \text{(corresponding angles)}\dots \left(1\right)\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow & \frac{A\mathrm{B/PQ}}{}=\frac{B\mathrm{C/}}{Q\mathrm{R.}}\\ \text{( corresponding sides)}\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow & \frac{A\mathrm{B/PQ}}{}=\; (\frac{BC/\mathrm{2)/(QR}}{/\mathrm{2)}}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \\ \Rightarrow & \frac{A\mathrm{B/PQ}}{}=\frac{B\mathrm{D/}}{Q\mathrm{M.}}\end{array}$$

$$\begin{array}{c}\left[\begin{array}{c}D\text{and}M\text{are mid points}\\ \text{of}BC\text{and}QR\end{array}\right]\dots \left(2\right)\end{array}$$

In $\Delta ABD,\Delta PQM$

$$\angle ABD=\angle PQM\dots \text{(from 1)}$$

$$\frac{A\mathrm{B/}}{PQ}=\frac{B\mathrm{D/}}{QM}\dots \text{(from 2)}$$

$$\begin{array}{cc}\Rightarrow & \Delta ABD\sim \Delta PQM\\ & \text{(SAS Criterion)}\end{array}$$ ⇒AB/PQ=BD/QM=AD/PM

(Corresponding sides)

$$\begin{array}{cc}\Rightarrow \frac{AB}{PQ}& =\frac{AD}{PM}\end{array}$$