Ex 6.4 Class 10 Maths Triangles

Triangles 

Class 10

 Ex 6.4

Maths

Q. 1. Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution:

Given

∆ABC ~ ∆DEF 

ar ∆ABC = 64 cm²

ar ∆DEF = 121 cm²

EF = 15.4 cm

Find 

BC = ?

We have 

∆ABC ~ ∆DEF 

$$\begin{array}{cc}\frac{\text{Ar of}\Delta ABC}{\text{/ Ar of}\Delta DEF}& =\frac{(BC{)²/}^{}}{(EF{)²}^{}}\end{array}$$

$$\begin{array}{c}\frac{64c{\mathrm{m²\; /}}^{}}{121c{\mathrm{m²\; =}}^{}}\end{array}$$(BC)²/ (15.4)²

BC² = [(15.4)² × 64] /121

BC = [15.4×8]/11

BC = 11.2cm

Q. 2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Solution:

In trapezium $ABCD,$ 

$AB\parallel CD$ and $AB=2CD$

Diagonals $AC,BD$ intersect at ‘$O$

In $\Delta AOB\text{and}\Delta COD$ 

$\angle AOB=\angle CO\mathrm{D \; \; \; \; \; \; (V.O.A.)}$

$\angle ABO=\angle CDO$(A.I.A.) 

$\Rightarrow \Delta AOB\sim \Delta COD$(AA criterion)

$\begin{array}{cc}\Rightarrow \frac{A\mathrm{r\; of\; \Delta AOB\; Ar\; of\; \Delta COD}}{}& =\frac{{(AB)²/}^{}}{{(CD)²}^{}}\end{array}$

$\begin{array}{cc}=\frac{{(2CD)²/}^{}}{{\left(CD\right)}^2}& =\frac{4C{\mathrm{D²/}}^{\mathrm{CD²}}}{}=\frac{\mathrm{4/}}{1}\end{array}$

Area of ΔAOB:Area of ΔCOD=4:1

Q 3. In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that: 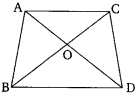ar(ABC)ar(DBC)=AO/DO

Solution:

In $\Delta ABC$

Draw $AM\perp BC$

In $\Delta DBC$

Draw $DN\perp BC$

Now in $\Delta AOM,\Delta DON$

$$\begin{array}{cc}& \angle AMO=\angle DNO={90}^{\circ }\end{array}$$

$$\begin{array}{c}\\ & \angle AOM=\angle DON\\ & \text{(V.O.A.)}\end{array}$$

$$\begin{array}{cc}\Rightarrow & \Delta AOM\sim \Delta DON\\ \text{(AA Criterion)}\end{array}$$

$$\begin{array}{c}\Rightarrow \frac{A\mathrm{M/DN}}{}=\frac{O\mathrm{M/}}{ON}=\frac{A\mathrm{O/}}{D\mathrm{O.}}\dots \left(1\right)\end{array}$$

Now,

$$\begin{array}{cc}ar\Delta ABC& =\frac{\mathrm{1/}}{2}\times \text{Base}\times \text{Height}\end{array}$$

$$\begin{array}{c}\\ & =\frac{1}{2}\times BC\times AM\end{array}$$

$$ar\Delta DBC=\frac{\mathrm{1/}}{2}\times BC\times DN$$

$$ar\Delta ABC/ar\Delta DBC\; =(\frac{\frac{\mathrm{1/}}{2}\times BC\times A\mathrm{M)/(}}{\frac{\mathrm{1/}}{2}\times BC\times D\mathrm{N)}}$$

$$\begin{array}{c}\frac{\mathrm{ar\Delta ABC/ar\Delta DBC}}{}\\ =\frac{A\mathrm{M/}}{DN}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ \frac{ar\Delta AB\mathrm{C/}}{ar\Delta DBC}& =\frac{A\mathrm{O/}}{DO}\dots \text{from}\left(1\right)\end{array}$$

Q. 4. If the areas of two similar triangles are equal, prove that they are congruent.
Solution:

Given:

$\Delta ABC\sim \Delta DEF$

$\mathrm{To\; Prove:}$

$\mathrm{\Delta ABC\; \cong \; \Delta DEF}$

$\mathrm{Proof:}$

ΔABC∼ΔDEF

AB/DE=BC/EF=CA/FD (SSS Criterion)

$$\begin{array}{cc}& ar\Delta ABC=ar\Delta DEF\end{array}$$

$$\begin{array}{c}\\ \Rightarrow & \frac{ar\Delta AB\mathrm{C/ar\Delta DEF}}{}=1\dots \left(1\right)\end{array}$$

But,

$$\begin{array}{cc}\frac{ar\Delta AB\mathrm{C/}}{ar\Delta DEF}& =\frac{{(AB)²/}^{}}{{(DE)²}^{}}\\ =\frac{{(BC)²/}^{}}{{(EF)²}^{}}& =\frac{{(CA)²/}^{}}{{(FD)²}^{}}\end{array}$$

From $\left(1\right)$

$$\begin{array}{cc}\frac{(AB{)²/}^{}}{(DE{)²}^{}}& =\frac{(BC{)²/}^{}}{(EF{)²\; =}^{}}\\ \frac{(CA{)²/}^{}}{(FD{)²}^{}}\\ =1\end{array}$$

$$\begin{array}{c}\\ \Rightarrow \frac{(AB{)²/}^{}}{(DE{)²}^{}}& =1\end{array}$$

$$\begin{array}{c}\\ \Rightarrow (AB{)²}^{}& =(DE{)²}^{}\end{array}$$

$$\begin{array}{c}\\ \Rightarrow AB& =DE\dots \left(2\right)\end{array}$$

Similarly,       

⇒   $BC=EF....\left(3\right)$

   $CA=FD\dots .\left(4\right)$

Now, in $\Delta ABC,\Delta DEF$

$AB=DE$    $\text{(from 2)}$

$BC=EF$(from 3)

$CA=FD$(from 4)

$$\begin{array}{cc}\Rightarrow & \Delta ABC\cong \; \Delta DEF\\ \text{(SSS congruency)}\end{array}$$

Q. 5. D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution:

Given:

In $\Delta ABC$, $\mathrm{D,}E$ are the midpoints of $AB,\; BC\; and\; AC$ respectively.

$$\begin{array}{cc}\Rightarrow & DE\parallel BC\text{and}DE=\frac{\mathrm{1/}}{2}BC\end{array}$$

$$\begin{array}{c}\\ & \text{(by mid-point theorem)}\end{array}$$

Again, $E$ is mid-point of $BC$

$$\Rightarrow DF\parallel BE\text{and}DF=BE$$

In quadrilateral $DFEB$

$$DF\parallel BE\text{and}DF=BE$$

 $DFEB$ is a parallelogram

$$\begin{array}{cc}\Rightarrow & \angle B=\angle F\dots \left(1\right)\end{array}$$

$$\begin{array}{c}\\ & \left[\begin{array}{c}\text{Opposite angles of a}\\ \text{parallelogram are equal}\end{array}\right]\end{array}$$

Similarly, we can prove that

$DFCE$ is a parallelogram

$$\begin{array}{cc}\Rightarrow & \angle C=\angle D\dots \left(2\right)\end{array}$$

$$\begin{array}{c}\\ & \left[\begin{array}{c}\text{Opposite angles of a}\\ \text{parallelogram are equal}\end{array}\right]\end{array}$$

Now,

In $\Delta DEF$ and $\Delta ABC$

$$\angle DEF=\angle ABC\dots \text{from (1)}$$

$$\angle EDF=\angle ACB\dots \text{from (2)}$$

$$\begin{array}{cc}\Rightarrow & \Delta DEF\sim \Delta CAB\\ & \text{[AA Criterion]}\end{array}$$

The ratio of the areas of two similar triangles is equal to the square of corresponding sides.

$$\begin{array}{cc}\frac{\text{ar}\Delta DE\mathrm{F/}}{\text{ar}\Delta ABC}& =\frac{{(DE)²/}^{}}{{(AC)²}^{}}\\ =\frac{{(EF)²/}^{}}{{(AB)²}^{}}\\ =\frac{{(DF)²/}^{}}{{(BC)²}^{}}\end{array}$$

$$\begin{array}{cc}\frac{\text{ar}\Delta DE\mathrm{F/}}{\text{ar}\Delta ABC}& =\frac{(DF{)²/}^{}}{(BC{)²}^{}}\\ =\frac{(\frac{\mathrm{1/}}{2}BC{)²/}^{}}{(BC{)²}^{}}\\ =\frac{B{\mathrm{C²/}}^{}}{4B{\mathrm{C²}}^{}}\\ =\frac{\mathrm{1/}}{4}\end{array}$$

The ratio of the areas of $\Delta DEF$ and $\Delta ABC$ is $1:4$

Q. 6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:

Given :

In $\Delta PQR$, $PM$ is the median and, in $\Delta ABC$ $AN$ is the median

$$\Delta PQR\sim \Delta ABC\dots \left(\text{Given}\right)$$

$$\begin{array}{cc}& \angle PQR=\angle ABC\dots \left(1\right)\end{array}$$

$$\begin{array}{c}\\ & \angle QPR=\angle BAC\dots \left(2\right)\end{array}$$

$$\begin{array}{c}\\ & \angle QRP=\angle BCA\dots \left(3\right)\end{array}$$

$$\begin{array}{c}\\ & \\ & \text{and}\end{array}$$

$$\begin{array}{c}\\ & \\ & \frac{P\mathrm{Q/}}{AB}=\frac{Q\mathrm{R/}}{BC}=\frac{R\mathrm{P/}}{CA}\dots \left(4\right)\end{array}$$

(∵ If two triangles are similar, then their corresponding angles are equal andcorresponding sides are in the same ratio)

$$\begin{array}{cc}\frac{ar\Delta PQ\mathrm{R/}}{ar\Delta ABC}& =\frac{{(PQ)²/}^{}}{{(AB)²}^{}}\\ =\frac{{(QR)²/}^{}}{{(BC)²}^{}}\\ =\frac{{(RP)²/}^{}}{{(CA)²}^{}}\end{array}$$

$$\begin{array}{c}\left[\text{from area side square theorem}\right]\end{array}\dots \left(5\right)$$

Now, In $\Delta PQM$ and $\Delta ABN$

$$\angle PQM=\angle ABN\dots \text{from (1)}$$

And 

$\begin{array}{c}\frac{P\mathrm{Q/}}{AB}=\frac{Q\mathrm{M/}}{BN}\end{array}$

$$\begin{array}{c}\frac{P\mathrm{Q/}}{AB}=\frac{Q\mathrm{R/}}{BC}=\frac{2Q\mathrm{M/}}{2BN}\end{array}$$

$M,N$ are mid points of $Q$ and $BC$

$$\Rightarrow \Delta PQM\sim \Delta ABN$$[ $SAS$ similarity]

$$\begin{array}{cc}\Rightarrow \frac{ar\Delta PQ\mathrm{M/ar\Delta ABN}}{}& =\frac{(PQ{)²/}^{}}{(AB{)²}^{}}\\ =\frac{(QM{)²}^{}}{(BN{)²}^{}}\\ =\frac{(PM{)²/}^{}}{(AN{)²}^{}}\\ \dots \left[\text{Theorem 6.6}\right]\end{array}$$

from $\left(5\right)$ and $\left(6\right)$

$\begin{array}{c}\frac{ar\Delta PQ\mathrm{R/}}{ar\Delta ABC}=\frac{{(PM)²/}^{}}{{(AN)²}^{}}\end{array}$

Q. 7.  Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:

Given:

$\Delta ABE$ is described on the side $AB$ of the square $ABCD$

AB = a

and

AC= a√2

Since $\Delta ABE$ and $\Delta DBF$ are equilateral triangles

$\Delta ABE\sim \Delta DBF$ [each angle in an equilateral triangle measures ${\mathrm{60°}}^{}$ ]

The ratio of the areas of two similar triangles is equal to the square of the ratio of the corresponding sides.

$$\begin{array}{cc}& \frac{ar\Delta AB\mathrm{E/}}{ar\Delta DBF}=\frac{{(AB)²/}^{}}{{(DB)²}^{}}\end{array}$$

$$\begin{array}{c}ar\Delta ABEar\Delta DBF=\frac{{(AB)²/}^{}}{{(\sqrt{2}AB)²}^{}}\end{array}$$

$$[\therefore \text{Diagonal of a square is}\sqrt{2}\times \text{side}]$$

$$\begin{array}{cc}& \frac{ar\Delta AB\mathrm{E/}}{ar\Delta DBF}=\frac{A{\mathrm{B²/}}^{}}{2A{\mathrm{B²}}^{}}\end{array}$$

$$\begin{array}{c}ar\Delta ABE/ar\Delta DBF=\frac{\mathrm{1/}}{2}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ \Rightarrow & ar\Delta ABE=\frac{\mathrm{1/}}{2}ar\Delta DBF\end{array}$$

Tick the correct answer and justify.

Q. 8. Tick the correct answer and justify

(i) ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(a) 2 :1   (b) 1:2   (c) 4 :1   (d) 1:4

Solution: 

$\mathrm{\Delta }ABC\sim \mathrm{\Delta }BDE$ $(\because \text{equilateral triangles)}$

The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

$$\begin{array}{cc}\frac{ar\Delta AB\mathrm{C/}}{ar\Delta BDE}& =\frac{(BC{)²/}^{}}{(BD{)²}^{}}\\ =\frac{(BC{)²/}^{}}{{(\frac{B\mathrm{C/}}{2})²}^{}}\end{array}$$

$$\begin{array}{cc}[D\text{is the}& \text{mid point}\text{of}BC]\end{array}$$

$$\begin{array}{c}\\ & =\frac{(BC{)²}^{}\times 4}{(BC{)²}^{}}\\ =4\end{array}$$

$$\begin{array}{c}ar\Delta ABE:ar\Delta BDE=4:1\end{array}$$

The answer is (c) $4:1$

(ii) Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3      (b) 4 : 9      (c) 81 : 16     

(d) 16 : 81

solution: 

We know that,

The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

$$ar\Delta (1)\; :\; ar\Delta (2)\; =(\mathrm{4)²}:(9{)²}^{}=16:81$$

The answer is (d) $16:81$