Solved Sample Paper Term 1: (21-22)
CBSE Class 10
MATHEMATICS (Standard) 041
Sample Paper Term 1:
Time Allowed: 90 minutes
Maximum Marks: 40
***********************************
Sol.
(By Om Jitender Singh Tomar)
***********************************
GENERAL INSTRUCTIONS:
1. The question paper contains three parts A, B and C
2. Section A consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
3. Section B consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
4. Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
5. There is no negative marking.
SECTION A
Section A consists of 20 questions of 1 mark each. Any 16 questions are to be attempted.
***********************************
1. The ratio of LCM and HCF of the least composite and the least prime numbers is
(a) 1:2
(b) 2:1
(c) 1:1
(d) 1:3
***********************************
Sol. 1
By Om Jitender Singh Tomar
Least composite number = 4 and
the least prime number = 2.
LCM(4, 2) : HCF(4, 2)
= 4:2
= 2:1
***********************************
2. The value of k for which the lines 5x + 7y = 3 and 15x + 21y = k coincide is
(a) 9
(b) 5
(c) 7
(d) 18
***********************************
Sol. 2
By Om Jitender Singh Tomar
For coincide lines :
𝑎₁/𝑎₂ = 𝑏₁/𝑏₂ = 𝑐₁/𝑐₂
so, 5/15 = 7/21 = −3/−k
i.e. k= 9
***********************************
3. A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is
(a)350m
(b) 250m
(c) 300m
(d) 225
***********************************
Sol. 3
By Om Jitender Singh Tomar
By Pythagoras theorem
The required distance
= √(200² + 150²)
= √(40000+ 22500)
= √(62500)
= 250m.
So the distance of the girl from the starting point is 250m.
***********************************
4. The lengths of the diagonals of a rhombus are 24cm and 32cm, then the length of the altitude of the rhombus is
(a) 12cm
(b) 12.8cm
(c) 19 cm
(d) 19.2cm
***********************************
Sol. 4
By Om Jitender Singh Tomar
By
Area of the Rhombus = 1/2d₁d₂
=1/2x 24 x 32
= 384 cm².
Using Pythagoras theorem
side² = (1/2d₁)² + (1/2d₂)²
= 12² +16²
= 144 +256
= 400
Side = √400cm
Side = 20cm
Area of the Rhombus = Base x Altitude
384 = 20 x Altitude
So Altitude = 384/20
= 19.2cm
***********************************
5. Two fair coins are tossed. What is the probability of getting at the most one head?
(a) 3/4
(b) 1/4
(c) 1/2
(d) 3/8
***********************************
Sol. 5
(By Om Jitender Singh Tomar)
Possible outcomes or Sample Space
= (HH), (HT), (TH), (TT)
Favorable outcomes(at the most one head) are = (HT), (TH), (TT)
So
P(E) of getting at the most one head = Favourable out Came / Total out Game
P(E) = 3/4
***********************************
6. ∆ABC~∆PQR. If AM and PN are altitudes of ∆ABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM:PN =
(a) 16:81
(b) 4:9
(c) 3:2
(d) 2:3
***********************************
Sol.
(By Om Jitender Singh Tomar)
For similar triangles
Ratio of Altitudes = Ratio of sides
So
AM:PN = AB:PQ
AM:PN = 2:3
***********************************
7. If 2sin2β – cos2β = 2, then β is
(a) 0ᵒ
(b) 90ᵒ
(c) 45ᵒ
(d) 30ᵒ
***********************************
Sol. 7
(By Om Jitender Singh Tomar)
2sin²β – cos²β = 2
Then
2 sin²β – (1– sin²β) = 2
= > 2 sin²β – 1+ sin²β = 2
= > 2 sin²β + sin²β = 2 + 1
= > 3 sin²β = 3
= > sin²β = 3/3
=> sin²β =1
=> sinβ =√1
=> sin β =1 ...(1)
We know that
=> sin 90ᵒ = 1 ...(2)
From equation (1) and (2)
β = 90ᵒ
***********************************
8. Prime factors of the denominator of a rational number with the decimal expansion 44.123 are
(a) 2,3
(b) 2,3,5
(c) 2,5
(d) 3,5
***********************************
Sol. 8
(By Om Jitender Singh Tomar)
Since it has a terminating decimal expansion,
so prime factors of the denominator will be 2, 5
***********************************
9. The lines x = a and y = b, are
(a) intersecting
(b) parallel
(c) overlapping
(d) (None of these)
***********************************
Sol. 9
(By Om Jitender Singh Tomar)
Lines x = a is a line parallel to y axis and y = b is a line parallel to x axis. So they
will intersect.
***********************************
10. The distance of point A(–5, 6) from the origin is
(a) 11 units
(b) 61 units
(c) √11 units
(d) √61 units
***********************************
Sol. 10
(By Om Jitender Singh Tomar)
Distance of point A(-5,6) from the origin O(0,0) is
AO = √[(0 + 5)² + (0 − 6)²]
AO = √(25 + 36)
AO = √61 units
***********************************
11. If a² = 23/25, then a is
(a) rational
(b) irrational
(c) whole number
(d) integer
***********************************
Sol. 11
(By Om Jitender Singh Tomar)
a²=23/25,
then a = √23/5
Which is irrational
***********************************
12. If LCM(x, 18) = 36 and HCF(x, 18) = 2, then x is
(a) 2
(b) 3
(c) 4
(d) 5
***********************************
Sol. 12
(By Om Jitender Singh Tomar)
Product of Two No. = LCM X HCF
18 X x = 36 X 2
x = (36 × 2)/18
x = 72/18
x = 4
***********************************
13. In ∆ABC right angled at B, if tan A= √3, then cos A cos C – sin A sin C =
(a) –1
(b) 0
(c) 1
(d) √3/2
***********************************
Sol. 13
(By Om Jitender Singh Tomar)
tan A= √3 ........ (1)
we know that
tan 60° = √3 ........ (2)
From equation (1) and (2)
so ∠A=60°,
Hence ∠C = 30°.
So
cos A cos C – sin A sin C
= (1/2)x (√3/2) – (√3/2)x (1/2)
= √3/4–√3/4
= 0
***********************************
14. If the angles of ∆ABC are in ratio 1:1:2, respectively (the largest angle being angle C), then the value of
(a) 0
(b) 1/2
(c) 1
(d) √3/2
***********************************
Sol. 14
(By Om Jitender Singh Tomar)
∠A = 1x
∠B = 1x
∠C = 2x
∠A + ∠B + ∠C =180°, (by ASPOT)
1x +1x +2x =180°
4x =180°
x = 180°/4
x = 45°.
Now
∠A = 1x × 45°
∠A = 45°
∠B = 1x × 45°
∠B = 45°
∠C = 2x × 45°
∠C = 90°
ATQ
= secA/cosec B– tanA/cot B
= sec 45/cosec 45– tan 45/cot 45
= √2/√2– 1/1
= 1–1
= 0
***********************************
15. The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is
(a) 22
(b) 24
(c) 75
(d) 40
***********************************
Sol. 15
(By Om Jitender Singh Tomar)
r = 0.7m
Total Distance = 176
Number of revolutions= Total distance/Circumference
= 176/(2×π×r)
= 176/(2×22/7× 0.7)
= 176/4.4
= 40 Revolution
***********************************
16. ∆ABC is such that AB=3 cm, BC= 2cm, CA= 2.5 cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is
(a) 7.5 cm
(b) 15 cm
(c) 22.5 cm
(d) 30 cm
***********************************
Sol. 16
(By Om Jitender Singh Tomar)
AB=3 cm,
BC= 2cm,
CA= 2.5 cm
EF = 4cm
Since ∆ABC ~ ∆DEF
p. of ∆ABC/ p. of ∆DEF= Side of ∆ABC/ side of ∆DEF
p. of ∆ABC/ p. of ∆DEF = BC/EF
7.5/p of ∆DEF = 2/4
2×p of ∆DEF = 4×7.5
p of ∆DEF = 30/2
. So perimeter of ∆DEF = 15cm
***********************************
17. In the figure, if DE∥ BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals
(a) 7cm
(b) 6cm
(c) 4cm
(d) 3cm
***********************************
Sol. 17
(By Om Jitender Singh Tomar)
AD = 3cm
BD = 4cm
BC= 14 cm
Since DE∥ BC,
∆ABC ~ ∆ADE ( By AA similarity)
So
AD/AB= DE/BC
i.e. 3/7= DE/14
So 7× DE = 14×3
DE = (14×3)/2
DE = 6cm
***********************************
18. If 4 tanβ = 3, then
(a) 0
(b) 1/3
(c) 2/3
(d) 3/4
***********************************
Sol.
(By Om Jitender Singh Tomar)
4 𝑠𝑖𝑛𝛽−3 cos𝛽 / 4 sin 𝛽+3 cos𝛽
Dividing both numerator and denominator by cosβ,
= (4 𝑠𝑖𝑛𝛽)/cosβ−(3 cos𝛽)/cosβ / (4 sin 𝛽)/cosβ + (3 cos𝛽)/cosβ
= (4 𝑡𝑎𝑛𝛽−3)/(4 tan 𝛽+3)
= (4×3/4−3)/(4×3/4+3)
= (3−3)/(3+3)
=0×6
=0
***********************************
19. One equation of a pair of dependent linear equations is –5x + 7y = 2. The second equation can be
(a) 10x+14y +4 = 0
(b) –10x –14y+ 4 = 0
(c) –10x+14y + 4 = 0
(d) 10x – 14y = –4
***********************************
Sol. 19
(By Om Jitender Singh Tomar)
=> –5x + 7y = 2
=> –2×(–5x + 7y = 2)
gives
=> 10x – 14y = –4
***********************************
20. A letter of English alphabets is chosen at random. What is the probability that it is a letter of the word ‘MATHEMATICS’?
(a) 4/13
(b) 9/26
(c) 5/13
(d) 11/26
**********************************
Sol.
(By Om Jitender Singh Tomar)
Number of Possible Total outcomes = 26
Sample Space = M, A, T, H, E, I, C, S
Favorable outcomes = (8)
P(E) For word MATHEMATICS = Favourable out Came / Total outcame
P(E) = 8/26
P(E) = 4/13
***********************************
SECTION B
Section B consists of 20 questions of 1 mark each. Any 16 questions are to be attempted.
21 If sum of two numbers is 1215 and their HCF is 81, then the possible number of pairs of such numbers are
(a) 2
(b) 3
(c) 4
(d) 5
***********************************
Sol.
(By Om Jitender Singh Tomar)
Since HCF = 81
Two numbers can be taken as 81x and 81y,
ATQ
81x + 81y = 1215
Or x+y = 15
which gives four co-prime pairs:
1,14
2,13
4,11
7, 8
***********************************
22 Given below is the graph representing two linear equations by lines AB and CD respectively. What is the area of the triangle formed by these two lines and the line x=0?
(a) 3sq. units
(b) 4sq. units
(c) 6sq. units
(d) 8sq. units
***********************************
Sol.
(By Om Jitender Singh Tomar)
Required Area of ∆ ACD = 1/2×Base × Height
= ½×(6)×2
= 6 sq units
***********************************
23 If tan α + cot α = 2, then tan²⁰α + cot²⁰α =
(a) 0 (b) 2 (c) 20 (d) 2²⁰
***********************************
Sol.
(By Om Jitender Singh Tomar)
tan α + cot α = 2
If α = 45°.
So
tan 45° + cot 45° = 2
1 + 1 = 2
Thus
tan α = cot α = 1
ATQ
= tan²⁰α + cot²⁰α
= (1)²⁰ + (1)²⁰
= 1+1
= 2
***********************************
24. If 217x + 131y = 913, 131x + 217y = 827, then x + y is
(a) 5 (b) 6 (c) 7 (d) 8
***********************************
Sol.
(By Om Jitender Singh Tomar)
217x + 131y = 913 .........(1)
131x + 217y = 827 .........(2)
Adding the equations (1) & (2) we will get:
348x + 348y = 1740.
Now
[348x + 348y = 1740] ÷ 348
So
x +y = 5
***********************************
25 The LCM of two prime numbers p and q (p > q) is 221. Find the value of 3p – q.
(a) 4 (b) 28 (c) 38 (d) 48
***********************************
Sol.
(By Om Jitender Singh Tomar)
LCM of two prime numbers = product of the numbers
p x q = 221
17 x 13 = 221
ATQ
⸫3p – q
= 3(17)–13
= 51–13
=38
***********************************
26 A card is drawn from a well shuffled deck of cards. What is the probability that the card drawn is neither a king nor a queen?
(a) 11/13
(b) 12/13
(c) 11/26
(d) 11/52
***********************************
Sol.
(By Om Jitender Singh Tomar)
Total number of cards without king and queen = 52 –8
= 44
P(E) for neither a king nor a queen
= favourable outcome / total outcome
= 44/52
= 11/13
***********************************
27 Two fair dice are rolled simultaneously. The probability that 5 will come up at least once is
(a) 5/36
(b) 11/36
(c) 12/36
(d) 23/36
***********************************
Sol.
(By Om Jitender Singh Tomar)
Outcomes when 5 will come up at least once are:
(1,5), (2,5), (3,5), (4,5), (5,5), (6,5), (5,1), (5,2), (5,3), (5,4) and (5,6)
Favourable outcame = 11
Total outcome = 36
P(E) that 5 will come up at least once = Favourable outcome / Total outcome
= 11/36
***********************************
28 If 1+ sin²α = 3 sinα cosα, then values of cot α are
(a) –1, 1
(b) 0,1
(c)1, 2
(d) –1,–1
***********************************
Sol.
(By Om Jitender Singh Tomar)
1+ sin²α = 3 sinα cos α
sin²α + cos²α + sin²α = 3 sinα cos α
2 sin²α – 3sinα cos α + cos²α = 0
2 sin²α – 2sinα cos α – 1sinα cos α + cos²α = 0
2 sinα( sinα – cos α) –cos α (sinα – cosα) = 0
(sinα – cos α)( 2sinα– cosα) =0
(sinα – cos α)=0 or ( 2sinα– cosα) =0
sinα = cos α or 2sinα = cosα
sinα/sinα = cosα/sinα or 2sinα/sinα = cosα/sinα
⸫1= cotα or 2 = cotα
⸫cotα = 1 or cotα = 2
***********************************
29 The vertices of a parallelogram in order are A(1,2), B(4, y), C(x, 6) and D(3,5). Then (x, y) is
(a) (6, 3)
(b) (3, 6)
(c) (5, 6)
(d) (1, 4)
***********************************
Sol.
(By Om Jitender Singh Tomar)
Since ABCD is a parallelogram, diagonals AC and BD bisect each other,
∴ mid point of AC= mid point of BD
[(𝑥+1)/2 , (6+2)/2] = [(3+4)/2 , (5+𝑦)/2]
Comparing the co-ordinates, we get,
(𝑥+1)/2 = (3+4)/2
x +1 = 7
. So,
x= 6
Similarly, (6+2)/2 = (5+𝑦)/2
5 + y = 8
y = 8 –5
y = 3
∴(x, y) = (6,3)
***********************************
30 In the given figure, ∠ACB = ∠CDA, AC = 8cm, AD = 3cm, then BD is
(a) 22/3 cm
(b) 26/3 cm
(c) 55/3 cm
(d) 64/3 cm
***********************************
Sol.
(By Om Jitender Singh Tomar)
∆ACD ~∆ ABC( AA )
∴ AC/AB = AD/AC (CPST)
8/AB = 3/8
This gives AB = 64/3 cm.
So
BD = AB – AD
BD = 64/3 –3
BD = 55/3cm.
***********************************
31 The equation of the perpendicular bisector of line segment joining points A(4,5) and B(–2,3) is
(a) 2x – y +7=0
(b) 3x +2 y – 7=0
(c) 3x – y – 7 =0
(d) 3x + y – 7=0
***********************************
Sol.
(By Om Jitender Singh Tomar)
A(4,5)
B(–2,3)
Any point (x, y) of perpendicular bisector will be equidistant from A & B.
∴ √[(𝑥 − 4)² + (𝑦 − 5)²]= √[(𝑥 + 2)² + (𝑦 −3)²]
squaring both sides
=> [(𝑥)² + (4)² – 2.𝑥.4 + (𝑦)² + (5)²– 2.𝑥.5 ]= [(𝑥)² + (2)² + 2.𝑥.2 + (𝑦)² + (3)² – 2.y.3]
=> 𝑥² + 16 – 8.𝑥 + 𝑦² + 25 – 10.y = 𝑥² + 4 + 4.𝑥 + 𝑦² + 9– 6.y
=> 𝑥² + 16 – 8.𝑥 + 𝑦² + 25 – 10.y – 𝑥² – 4 – 4.𝑥 – 𝑦² – 9 + 6.y = 0
=> 16 – 8.𝑥 + 41 – 10.y – 4.𝑥 – 13 + 6.y = 0
=> –12.𝑥 – 4y + 28=0
[–12.𝑥 – 4y + 28=0 ] ÷ 4
or
3 𝑥 + y – 7 = 0
***********************************
32 In the given figure, D is the mid-point of BC, then the value of cot 𝑦° cot 𝑥° is
(a) 2***********************************
Sol.
(By Om Jitender Singh Tomar)
CD = BD = BC/2
cot 𝑦°/cot 𝑥°= (B/ P)/(B/P)
cot 𝑦°/cot 𝑥°= (AC/BC)/(𝐴𝐶/𝐶𝐷)
= CD/BC
= CD/2CD
= 1/2
***********************************
33 The smallest number by which 1/13 should be multiplied so that its decimal expansion terminates after two decimal places is
(a) 13/100
(b) 13/10
(c) 10/13
(d) 100/13
***********************************
Sol.
(By Om Jitender Singh Tomar)
The smallest number by which 1/13 should be multiplied so that its decimal expansion terminates after two decimal points is 13/100 as
1/13 × .𝑥 = 13/100
.𝑥 = 1/100
.𝑥 = 0.01
Ans: 13/100
***********************************
34 Sides AB and BE of a right triangle, right angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is

(a) 32/3cm
(b) 16/3cm
(c)8/3cm
(d) 4/3cm
***********************************
Sol.
(By Om Jitender Singh Tomar)
∆ABE is a right triangle & FDGB is a
square of side .𝑥 cm
∆AFD ~∆ DGE( AA )
∴ AF/DG = FD/GE (CPST)
(16 − .𝑥)/.𝑥 = .𝑥/(8 − .𝑥) (CPST)
128 = 24 .𝑥
.𝑥 = 128/24
or .𝑥 = 16/3cm
***********************************
35 Point P divides the line segment joining R(–1, 3) and S(9,8) in ratio k:1. If P lies on the line x – y +2=0, then value of k is
(a) 2/3
(b) 1/2
(c) 1/3
(d) 1/4
***********************************
Sol. 35
(By Om Jitender Singh Tomar)
Since P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1 ∴ coordinates of
P =[ (9k −1)/(k+1)], [(8k+3)/(k+1)]
Since P lies on the line x – y +2 = 0, then [(9k −1)/(k+1)]–[(8k+3)/(k+1)]
+ 2 =0
(9k –1) – (8k+3) +2(k+1) = 0
k + 1
(9k –1) – (8k–3) +2(k+1) = 0
9k –1 – 8k–3 +2k + 2 = 0
3k – 2 = 0
3k = 2
k=2/3
***********************************
36. In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is
(a) 44cm²
(b) 49 cm²
(c) 98 cm²
(d) 49π/2 cm²
***********************************
Sol.
(By Om Jitender Singh Tomar)
side of square = 14 cm
r = 14/2 cm
r = 7 cm
Total Shaded Area = Area of semicircle + (Area of half square – Area of two quadrants)
= Area of semicircle + (Area of half
square – Area of semicircle)
= Area of half square
= ½ x 14 x14
= 98cm²
***********************************
37 Given below is the picture of the Olympic rings made by taking five congruent circles of radius 1cm each, intersecting in such a way that the chord formed by joining the point of intersection of two circles is also of length 1cm. Total area of all the dotted regions assuming the thickness of the rings to be negligible is
(a) 4(π/12 – √3/4) cm²(b) (π/6 – √3/4) cm²
(c) 4(π/6 – √3/4) cm²
(d) 8(π/6 – √3/4) cm²
***********************************
Sol.
(By Om Jitender Singh Tomar)
Let O be the center of the circle.
OA = OB = AB = 1cm.
So ∆OAB is an equilateral triangle and 8 segment of the circle.
∴ ∠AOB =60°
Required Area= 8 x Area of one segment with
r = 1cm,
θ = 60°
Total ar = 8×[ar of sector – ar of an equilateral ∆OAB]
Total ar = 8×[( θ/360)× π × r² – √3/4 (side)²]
= 8×[( 60/360)× π × r² – √3/4 (1)²]
= 8(π/6 – √3/4)cm²
***********************************
38 If 2 and ½ are the zeros of px² + 5x + r, then
(a) p = r = 2
(b) p = r = – 2
(c) p = 2, r= –2
(d) p = –2, r= 2
***********************************
Sol.
(By Om Jitender Singh Tomar)
px² + 5x + r
α = 2
β = 1/2
a = p
b = +5
c = r
Sum of zeroes
α + β = – b / a
2 + ½ = –5/p
i.e. 5/2 = –5/p
So p= –2
Product of zeroes
α × β = c / a
2 × ½ = r/p
i.e. r/p = 1
r = p
r = –2
***********************************
39 The circumference of a circle is 100 cm. The side of a square inscribed in the circle is
(a) 50√2 cm
(b) 100/π cm
(c) 50√2/π cm
(d) 100√2/π cm
***********************************
Sol.
(By Om Jitender Singh Tomar)
Circumference of a circle = 100 cm
2πr =100.
So
2r =100/π
2r = diagonal of the square.
diagonal of the square (2r) = side√2
side√2 = 100/π
∴ side = 100/√2.π
side = 50√2/π
***********************************
40 The number of solutions of 3x+y =243 and 243x–y = 3 is
(a) 0
(b) 1
(c) 2
(d) infinite
***********************************
Sol.
(By Om Jitender Singh Tomar)
3x+y =243
3x+y = 3⁵
By BSPS rule
x + y =5 ------------------(1)
243x–y = 3
(3⁵)x–y = 3
35x–5y = 3
By BSPS rule
5x – 5y =1 --------------------(2)
Since :
𝑎₁/𝑎₂ ≠ 𝑏₁/ 𝑏₂
so it has unique solution.
***********************************
SECTION C
Case study based questions:
Section C consists of 10 questions of 1 mark each. Any 8 questions are to be attempted.
Q 41-Q 45 are based on Case Study –1
The figure given alongside shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola.
Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time‘t’ in seconds is given by the polynomial h(t) such that
h(t) = –16t² + 8t + k.
41 What is the value of k?
(a) 0
(b) – 48
(c) 48
(d) 48/–16
***********************************
Sol.
(By Om Jitender Singh Tomar)
Initially, at t = 0,
Annie’s height = 48ft
So, at t =0,
h should be equal to 48
h(0) = –16(0)² + 8(0) + k = 48
So k = 48
***********************************
42 At what time will she touch the water in the pool?
(a) 30 seconds
(b) 2 seconds
(c) 1.5 seconds
(d) 0.5 seconds
***********************************
Sol.
(By Om Jitender Singh Tomar)
When Annie touches the pool, her height = 0 feet
i.e. –16t² + 8t + 48 =0 above water level
2t² – t – 6 =0
2t² – 4t +3t – 6 =0
2t(t – 2) + 3(t – 2) =0
(2t +3) (t – 2) =0
For. zero's
(2t +3) = 0 & (t – 2) = 0
2t +3 = 0 & t – 2 = 0
2t = – 3 & t = 2
t = – 3/2 & t = 2
i.e. t = 2 or t = –3/2
Since time cannot be negative ,
so t= 2 seconds
***********************************
43 Rita’s height (in feet) above the water level is given by another polynomial p(t) with zeroes –1 and 2. Then p(t) is given by-
(a) t² + t – 2.
(b) t² + 2t – 1
(c) 24t² – 24t + 48.
(d) –24t² + 24t + 48.
***********************************
Sol.
(By Om Jitender Singh Tomar)
t = –1 & t = 2 are the two zeroes of the polynomial p(t)
Then p(t)=k (t –1)(t – 2)
= k(t +1)(t – 2)
When t = 0 (initially) h₁ = 48ft
p(0) = 48
k (0²– 0 – 2)= 48
i.e. – 2k = 48
So the polynomial is –24(t² –t – 2)
= –24t² + 24t + 48.
***********************************
44 A polynomial q(t) with sum of zeroes as 1 and the product as -6 is modelling Anu’s height in feet above the water at any time t( in seconds). Then q(t) is given by
(a) t² + t + 6
(b) t² + t – 6
(c) –8t² + 8t + 48
(d) 8t² – 8t + 48
***********************************
Sol.
(By Om Jitender Singh Tomar)
A polynomial q(t) with sum of zeroes as 1 and the product as –6 is given by
q(t) = k(t² – (sum of zeroes)t + product of zeroes)
= k(t² –1t + (–6) ………..(1)
When t = 0 (initially)
q (0) = 48ft
q(0)=k(0²– 1(0) –6)= 48
i.e. –6k = 48
=> k= –8
Putting k = –8 in equation (1), reqd. polynomial is –8[t² –1t + (–6)]
= –8t² + 8t + 48
***********************************
45 The zeroes of the polynomial r(t) = –12t² + (k–3)t +48 are negative of each other. Then k is
(a) 3
(b) 0
(c) -1.5
(d) -3
***********************************
Sol.
(By Om Jitender Singh Tomar)
When the zeroes are negative of each other,
sum of the zeroes = 0
So, –b/a = 0
– (k – 3)/ −12 = 0
(k−3)/12 = 0
(k−3) = 0 ×12
k –3 = 0,
i.e. k = 3.
***********************************
Q 46–Q 50 are based on Case Study -2
CASE STUDY -2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.
It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.
Each team plays with 11 players on the field during the game including the goalie.
Positions you might play include-
* Forward: As shown by players A, B, C and D.
* Midfielders: As shown by players E, F and G.
* Fullbacks: As shown by players H, I and J.
* Goalie: As shown by player K
Using the picture of a hockey field below, answer the questions that follow:
46 The coordinates of the centroid of ΔEHJ are
(a) (–2/3, 1)
(b) (1,–2/3)
(c) (2/3,1)
(d) ( –2/3,–1)
***********************************
Sol.
(By Om Jitender Singh Tomar)
Centroid of ΔEHJ with E(2,1), H(-2,4) & J(-2,-2) is
[{2 + (−2)+ −2}/3] , [(1+4+ −2)/3]
= [{2 −2 −2}/3] , [(5 −2)/3]
= (−2/3) , (3/3)
= (–2/3, 1)
***********************************
47 If a player P needs to be at equal distances from A and G, such that A, P and G are in straight line, then position of P will be given by
(a) (–3/2, 2)
(b) (2,–3/2)
(c) (2, 3/2)
(d) ( –2,–3)
***********************************
Sol.
(By Om Jitender Singh Tomar)
If P needs to be at equal distance from A(3,6) and G(1,–3), such that A,P and G are collinear, then P will be the mid-point of AG.
So coordinates of P will be
[(3+1)/2 , (6+ −3)/2]
[(4)/2 , (3)/2]
= (2, 3/2)
***********************************
48 The point on x axis equidistant from I and E is
(a) (1/2, 0)
(b) (0,–1/2)
(c) (–1/2,0)
(d) ( 0,1/2)
***********************************
Sol.
(By Om Jitender Singh Tomar)
Let the point on x axis equidistant from I(-1,1) and E(2,1) be (x,0)
then
√[(𝑥 + 1)² + (0 − 1)²] = √[(𝑥 − 2)² + (0 − 1)²]
x² + 1 + 2x +1 = x² + 4 – 4x +1
2x + 2 = –4x +5
2x +4x = +5 –2
6x = 3
x = 3/6
So x = ½ .
∴ the required point is (½, 0)
***********************************
49 What are the coordinates of the position of a player Q such that his distance from K is twice his distance from E and K, Q and E are collinear?
(a) (1, 0)
(b) (0,1)
(c) (–2,1)
(d) ( –1,0)
***********************************
Sol.
(By Om Jitender Singh Tomar)
Let the coordinates of the position of a player Q such that his distance from K(–4,1) is twice his distance from E(2,1) be Q(x, y)
Then KQ : QE = 2: 1
Q(x, y) = [{(2×2 + 1×−4)/3} , {(2×1+1×1)/3}]
= [(4 −4)/3] , [(2+1)/3]
= [0/3 , 3/3]
= (0,1)
***********************************
50 The point on y axis equidistant from B and C is
(a) (–1, 0)
(b) (0,–1)
(c) (1,0)
(d) ( 0,1)
***********************************
Sol.
(By Om Jitender Singh Tomar)
Let the point on y axis equidistant from B(4,3) and C(4,-1) be (0,y)
then
√(4−0)² + (3−𝑦)² = √(4−0)² + (𝑦+1)²
√(4)² + (3−𝑦)² = √(4)² + (𝑦+1)²
16 + y² + 9 – 6y = 16 + y² + 1 + 2y
25 – 6y = 17 + 2y
– 6y –2y = 17 – 25
–8y = –8
So y = 1 .
∴ the required point is (0, 1)
***********************************
From CBSE board site
by Om Jitendra Singh Tomar


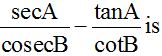

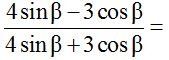







Post a Comment
Post a Comment