Q. 1. In the given figure (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
Solution:
As we all know the Basic Proportionality Theorem (B.P.T) or (Thales Theorem)
Two triangles are similar if :
(i) Their corresponding angles are equal
(ii) Their corresponding sides are in the same ratio (or proportion)
Proof (1):
(i) InΔABC
BC||DE
InΔABC & ΔADE
∠ABC = ∠ADE
(∵ Correspondinga angles)
∠ACB=∠AED
(∵Corresponding angles)
∠A = ∠A (Common)
⇒ΔABC ∼ ΔADE
AD/DB=AE/EC
1.5/3 = 1/EC
EC = (3×1)/1.5
EC = 2cm
Proof (2):
(ii) InΔABC
BC||DE
InΔABC & ΔADE
∠ABC = ∠ADE
(∵ Correspondinga angles)
∠ACB=∠AED
(∵Corresponding angles)
∠A = ∠A (Common)
⇒ΔABC ∼ ΔADE
AD/DB=AE/EC
AD/7.2 = 1.8/5.4
AD = (1.8 × 7.2)/5.4
AD = 2.4 cm
Q. 2. E and F are points on the sides PQ and PR respectively of a ∆PQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Solution:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(i) Proof (1):
As we know that a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side (by converse of BPT)
Steps:

Here,
PE/EQ = PF/FR
3.9/3 = 3.6/2.4
1.3cm ≠ 1.5cm
Hence,
PE/EQ ≠ PF/FR
According to converse of BPT, EF is not parallel to QR.
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(ii) Proof:

Here
As we know that a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side (by converse of BPT)
Here,
PE/EQ = PF/FR
4/4.5 = 8/9
40/45 = 8/9
8/9 = 8/9
1.3cm = 1.5cm
Hence,
PE/EQ = PF/FR
According to converse of BPT, EF is parallel to QR.
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
(ii) Proof:

Here
As we know that a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side (by converse of BPT)
Here,
PQ = 1.28 and PE = 0.18
EQ = PQ – PE = 1.28 – 0.18 = 1.10
PR = 2.56 and PF = 0.36
FR = PR – PF = 2.56 – 0.36 = 2.20
Now,
PE/EQ = PF/FR
0.18/1.10 = 0.36/2.20
18/110 = 36/230
9/55 = 9/55
Hence,
PE/EQ = PF/FR
According to converse of BPT, EF is parallel to QR.
3. In the given figure, if LM || CB and LN || CD. Prove that 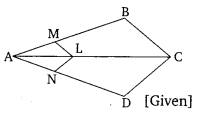
Solution:
As we know if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Steps:
In ΔABC, LM || CB
AM/MB = AL/LC …(
In ΔACDL, LN || CD
AN/DN=AL/LC …(2) (by BPT)
From equations (1) and (2)
AM/MB=AN/DN
⇒MB/AM=DN/AN
Adding 1 on both sides
MB/AM+1=DNA/N+1
(MB+AM)/AM=(DN+AN)/AN
AB/AM=AD/AN
or
AM/AB=AN/AD
Q. 4. In the given figure, DE || AC and DF || AE.
Prove that 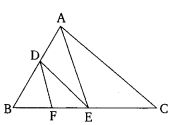
Solution:
As we know if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Steps:
In ΔABC
DE||AC
BD/AD=BE/EC. …(i) (by BPT)
InΔABE
DF||AE
BD/AD=BF/FE. …(ii) (by BPT)
From (i and (i
BD/AD=BE/EC=BF/FE
BE/EC=BF/FE
Q. 5. In the given figure, DE || OQ and DF || OR. Show that EF || QR.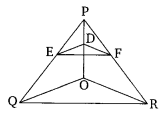
Solution:
As we know if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Steps:
In ΔPOQ
DE||OQ (Given)
PE/EQ=PD/OD
In ΔPOR
DF||OR(Given)
PF/FR=PD/DO. …(2)
From (1) & (2)
In ΔPQR
PE/EQ=PF/FR
∴QR || EF (Converse of BPT)
Q 6. In the given figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.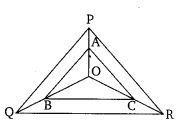
Solution:
As we know if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
In ΔOPQ
AB||PQ(Given)
OA/AP=OB/BQ. …(i)
[∵ Thales Theorem (BPT)]
In ΔOPR
AC||PQ(Given)
OA/AP=OC/CR …(ii)
[ ∵Thales Theorem (BPT)]
From (i & (ii)
OA/AP=OB/BR=OC/CR
OB/BQ=OC/CR
Now In ΔOQR
OB/BQ=OC/CR
BC||QR [∵ Converse of BPT]
Q.7 Using B.P.T., prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that your have proved it in class IX)
Solution:
We know that theorem 6.1 states that “If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio (BPT)”.
Given:
In ΔABC ,D is the midpoint of AB and DE||BC
To Prove:
AE = EC
Proof:
In ΔABC ,D is the midpoint of AB and DE||BC
Therefore,
AD=BD
AD/BD=1
Now,
DE||BC
⇒AE/EC=AD/BD [Theorem6.1]
⇒AE/EC =1
⇒AE = EC
Hence ,
Point E is the midpoint of AC.
Q 8. Using converse of B.P.T., prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that your have done it in class IX)
Solution:
We know that theorem 6.2 tells us if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side. (Converse of BPT)
In ΔABC
D is the midpoint of AB
AD = BD
AD/BD = 1 …(i)
E is the midpoint of AC
AE = CE
AE/BE = 1 …(ii)
From (i) and (ii)
AD/BD=AE/BE=1
AD/BD=AE/BE
According to theorem 6.2, (Converse of BPT)
DE || BC
Q 9.ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O.
Show that
Solution:
Given: ABCD trapezium in which AB||CD. AC and BD intersect at ‘O′.
To Prove: OA/OB=OC/OD
Construct : EO parallel to AB and C (EO∥AB(EO∥CD) through ‘O′.
In ΔABC
OE||AB(∵Construction)
According to theorem 6.1 (BPT)
BE/CE=OA/OC. …(i)
In ΔBCD
OE||CD(∵Construction
According to theorem 6.1 (BPT)
BE/CE=OB/OD…(ii)
From (i and (ii)
OA/OC=OB/OD
⇒OA/OB=OC/OD
Q. 10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that
Solution:
As we know if a line divides any two sides of a triangle in the same ratio,then the line is parallel to the third side.
Given: A quadrilateral ABCD
with Diagonals AC, BD intersect at ‘O′.
Draw EF || AB
In ΔABC
OE || AB
⇒OA/OC = BE/CE (BPT) ⋯(1)
But OA/OB = OC/OD (Given)
⇒OA/OC = OB/OD …(2)
From (1 and (2)
OB/OD=BE/CE
In ΔBCD
OB/OD=BE/CE
OE||CD
(buy Converse of BPT)
OE||AB and OE||CD
⇒AB||CD
⇒ABCD is a trapezium







Post a Comment
Post a Comment