Ex 6.5 Class 10 Maths Triangles

Triangles 

Class 10 

Ex 6.5

Q. 1. Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution:

(i) 25²= 7²+24²

625= 48+576

625=625

These sides of triangle formed right angle triangle with hypotenuse 25.

(ii) 8²= 3²+6²

64= 9+36

64 ≠ 45

These sides of triangle does not formed right angle triangle.

(iii) 100²= 50²+80²

10,000= 2500+6400

10,000 ≠ 8500

These sides of triangle does not formed right angle triangle.

(iv) 13²= 5²+12²

169= 25+144

169=169

These sides of triangle formed right angle triangle with hypotenuse 13.

Q. 2. PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM×MR.
Solution:

First Method:

= PM²/RM²

Second Method

In $\Delta PQR;$

$\angle QPR={\mathrm{90°}}^{}$ and $PM\perp QR$

In $\Delta PQR$ and $\Delta MQP$

$$\begin{array}{cc}& \angle QPR=\angle QMP={\mathrm{90°}}^{}\end{array}$$

$$\begin{array}{c}\\ & \angle PQR=\angle MQP\\ \text{(Common Angles)}\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow & \Delta PQR\sim \Delta MQP\\ \text{(AA Criterion)}\dots \left(1\right)\end{array}$$

In $\Delta PQR$ and $\Delta MPR$

$$\begin{array}{cc}& \angle QMP=\angle PMR={\mathrm{90°}}^{}\end{array}$$

$$\begin{array}{c}\\ & \angle PRQ=\angle RPM\\ & \text{(Common Angles)}\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow & \Delta PQR\sim \Delta MPR\\ \text{(AA Criterion)}\dots \left(2\right)\end{array}$$

From $\left(1\right)$ and $\left(2\right)$

$$\begin{array}{cc}& \Delta MQP\sim \Delta MPR\end{array}$$

$$\begin{array}{c}\\ & \frac{P\mathrm{M/}}{MR}=\frac{Q\mathrm{M/}}{PM}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \left[\begin{array}{c}\text{Comparing sides}\\ \text{opposite to equal angles}\end{array}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ \Rightarrow & P{\mathrm{M²}}^{}=Q\mathrm{M\times }MR\end{array}$$

Q. 3. In the given figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that

(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD² = BD.CD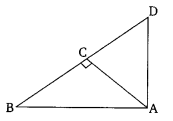

Solution:

Steps:

(i) In $\Delta BAD\text{and}\Delta BCA$

$\mathrm{\angle B\; =\; \angle B\; (Common\; Angles)}$

$\mathrm{\angle BAD\; =}$∠BCA  (90°)

$$\begin{array}{cc}& \Rightarrow \Delta BAD\sim \; \Delta BCA\mathrm{(AA\; Similarity)}\end{array}$$

$$\begin{array}{c}\\ & \\ & \Rightarrow A\frac{\mathrm{B/BD}}{}=\frac{\mathrm{BC}/}{AB}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \left[\begin{array}{c}\text{Corresponding sides}\\ \text{of similar triangle}\end{array}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ & \Rightarrow A{\mathrm{B²}}^{}=BC\cdot BD\end{array}$$

(ii) 

In ΔBAD and ΔBCA 

∠B = ∠B (Common Angles)

∠BAD = ∠BCA (90°)

⇒ΔBAD ∼ ΔBCA (AA Similarity) ...(1)

 In $\Delta \mathrm{ABD}\text{and}\Delta ACD$

$$\begin{array}{cc}& \angle D\; =\; \angle D\; (Common\; Angles)\end{array}$$

ty)...(2)

(2)

$$\begin{array}{c}\\ & \\ & \Rightarrow \Delta ACB\sim \Delta ACD\end{array}$$

$$\begin{array}{c}\frac{\mathrm{AC/CD}}{}=\frac{\mathrm{BC}/}{\mathrm{AC}}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \left[\begin{array}{c}\text{Corresponding sides}\\ \text{of similar triangle}\end{array}\right]\end{array}$$

AC²=BC⋅CD

(iii) 

 In $\Delta \mathrm{ABD}\text{and}\Delta ACD$

$$\begin{array}{cc}& \angle D\; =\; \angle D\; (Common\; Angles)\end{array}$$

$$\begin{array}{c}\angle BAD\; =\; \angle DCA\; (90°)\end{array}$$

$$\begin{array}{c}\Rightarrow \Delta BAD\; \sim \; \Delta BCA\; (AA\; Similari\end{array}$$ty)

$$\begin{array}{c}\Rightarrow \Delta BCA\sim \Delta ACD\end{array}$$

$$\begin{array}{c}\\ & \\ & \Rightarrow AD\frac{/}{\mathrm{CD\; =\; BD/AD}}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & \left[\begin{array}{c}\text{Corresponding sides}\\ \text{of similar triangle}\end{array}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ & \Rightarrow \mathrm{AD}{²}^{}=\; CD\cdot BD\end{array}$$

Q. 4. ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².
Solution:

Given:

In $\Delta ABC,$

$\angle ACB={\mathrm{90°}}^{}$ and $AC=BC$

But

$$\begin{array}{cc}A{\mathrm{B²}}^{}& =A{\mathrm{C²}}^{}+B{\mathrm{C²}}^{}\end{array}$$

$$\begin{array}{c}AB²\; =A{\mathrm{C²}}^{}+A{\mathrm{C²}}^{}[\because \; AC=BC]\end{array}$$

$$\begin{array}{c}\\ A{\mathrm{B²}}^{}& =2A{\mathrm{C²}}^{}\end{array}$$

Q. 5. ABC is an isosceles triangle with AC = BC. If AB² = 2AC² , Prove that ABC is a right triangle.
Solution:

Given: 

In $\Delta ABC$

$$AC=BC$$

And

$$\begin{array}{cc}A{\mathrm{B²}}^{}& =2A{\mathrm{C²}}^{}\end{array}$$

$$\begin{array}{c}\\ & AB²\; =A{\mathrm{C²}}^{}+A{\mathrm{C²}}^{}\end{array}$$

$$\begin{array}{cc}& =A{\mathrm{C²}}^{}+B{\mathrm{C²}}^{}[\because AC=BC]\end{array}$$

$\Rightarrow \angle ACB={\mathrm{90°}}^{}$

$\begin{array}{r}\Rightarrow \mathrm{\Delta }ABC\end{array}$ is a right triangle

Q. 6. ABC is an equilateral triangle of side 2a. Find each of its altitudes.

Solution:

Given: 

Sn equilateral triangle of side 2a.

So in $\Delta ABC$

$AB=BC=CA=2a$

$AD\perp BC$ 

$$\begin{array}{cc}\Rightarrow BD& =CD=\frac{\mathrm{1/}}{2}BC=a\end{array}$$

(because D is the midpoint of BC)

In $\Delta ADB$ , 

$$\begin{array}{cc}A{\mathrm{B²}}^{}& =A{\mathrm{D²}}^{}+B{\mathrm{D²}}^{}\end{array}$$

$$\begin{array}{c}{\mathrm{AD²}}^{}\\ =A{\mathrm{B²}}^{}-B{\mathrm{D²}}^{}\end{array}$$

$$\begin{array}{c}=\; (2a{)²\; –}^{}{\mathrm{a²}}^{}\end{array}$$

$$\begin{array}{c}\\ & =4{\mathrm{a²\; –\; a²}}^{}\end{array}$$

$$\begin{array}{c}\\ & =3{\mathrm{a²}}^{}\end{array}$$

$$\begin{array}{c}AD\; =\sqrt{3}a\end{array}$$ Units 

Q. 7. Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Solution:

Given:  a rhombus ABCD the diagonals AC and BD bisect each other at O.

AB = BC = CD = AD

$AC\perp BD$ and $OA=OC;$OB = OD 

To prove:

AB²+BC²+CD²+AD²=AC²+BD²

In rhombus $ABCD$

$AC\perp BD$ and $OA=OC;$OB = OD 

In $\Delta AO\mathrm{B,}$∠AOB=90∘

$\Rightarrow A{\mathrm{B²}}^{}=O{\mathrm{A²}}^{}+O{\mathrm{B²}}^{}\dots \left(1\right)$

$\Rightarrow A{\mathrm{B²}}^{}=¼{\mathrm{AC²}}^{}+¼{\mathrm{BD²}}^{}$

² + AD² = AC²+BD²

proved

Or

Given:  a rhombus ABCD the diagonals AC and BD bisect each other at O.

AB = BC = CD = AD

$AC\perp BD$ and $OA=OC;$OB = OD 

To prove:

AB²+BC²+CD²+AD²=AC²+BD²

In rhombus $ABCD$

$AC\perp BD$ and $OA=OC;$OB = OD 

In $\Delta AO\mathrm{B,}$∠AOB=90∘

$A{\mathrm{B²}}^{}=O{\mathrm{A²}}^{}+O{\mathrm{B²}}^{}\dots \left(1\right)$

$$\begin{array}{c}B{\mathrm{C²}}^{}=O{\mathrm{B²}}^{}+O{\mathrm{C²}}^{}\dots \left(2\right)\end{array}$$

$$\begin{array}{c}\\ C{\mathrm{D²}}^{}=O{\mathrm{C²}}^{}+O{\mathrm{D²}}^{}\dots \left(3\right)\end{array}$$

$$\begin{array}{c}\\ A{\mathrm{D²}}^{}=O{\mathrm{D²}}^{}+O{\mathrm{A²}}^{}\dots \left(4\right)\end{array}$$

Adding $\left(1\right),\left(2\right),\left(3\right)$ and $\left(4\right)$

$$\begin{array}{cc}& A{\mathrm{B²}}^{}+B{\mathrm{C²}}^{}+C{\mathrm{D²}}^{}+A{\mathrm{D²}}^{}\\ =\left[\begin{array}{c}O{\mathrm{A²}}^{}+O{\mathrm{B²}}^{}+O{\mathrm{B²}}^{}+O{\mathrm{C²}}^{}+\\ O{\mathrm{C²}}^{}+O{\mathrm{D²}}^{}+O{\mathrm{D²}}^{}+O{\mathrm{A²}}^{}\end{array}\right]\end{array}$$

$$\begin{array}{c}\\ & =2O{\mathrm{A²}}^{}+2O{\mathrm{B²}}^{}+2O{\mathrm{C²}}^{}+2O{\mathrm{D²}}^{}\end{array}$$

$$\begin{array}{c}\\ & =2[O{\mathrm{A²}}^{}+O{\mathrm{B²}}^{}+O{\mathrm{C²}}^{}+O{\mathrm{D²}}^{}]\end{array}$$

$$\begin{array}{c}\\ & =2[{(\frac{A\mathrm{C/2}}{})²}^{}+{(\frac{B\mathrm{D/2}}{})²}^{}+{(\frac{A\mathrm{C/}}{2})²}^{}+{(\frac{B\mathrm{D/}}{2})²}^{}]\end{array}$$

$$\begin{array}{c}\\ & \\ & OA\end{array}$$= OC = AC/2 and OB = OD = BD/2

$$\begin{array}{c}\frac{}{}\\ & \\ & =2[(\frac{A{\mathrm{C²}}^{}+B{\mathrm{D²}}^{}+A{\mathrm{C²}}^{}+B{\mathrm{D²)/}}^{}}{4}]\end{array}$$

$$\begin{array}{c}\\ & =2[(\frac{2A{\mathrm{C²}}^{}+2B{\mathrm{D²)/}}^{}}{4}]\end{array}$$

$$\begin{array}{c}\\ & =4[(\frac{A{\mathrm{C²}}^{}+B{\mathrm{D²)/}}^{}}{4}]\end{array}$$

$$\begin{array}{c}\\ & =A{\mathrm{C²}}^{}+B{\mathrm{D²}}^{}\end{array}$$

AB²+BC²+CD²+AD²=AC²+BD²

Q. 8. In the given figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF².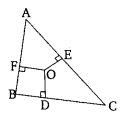

Solution:

Given: 

(i) In $\Delta ABC$

$OD\perp BC,OE\perp AC$ and $OF\perp AB$

Construction;

$\mathrm{joined\; O}A,OB$ and $O\mathrm{C.}$

In $\Delta OAF$

 $\begin{array}{cc}O{\mathrm{A²}}^{}& =A\mathrm{F²}+O{\mathrm{F²}}^{}\cdots \left(1\right)\\ [\because \angle OFA={\mathrm{90°}}^{}]\end{array}$

Similarly, In $\Delta OBD$

$\begin{array}{cc}O{\mathrm{B²}}^{}& =B\mathrm{D²}+O{\mathrm{D²}}^{}\cdots \left(2\right)\\ [\because \angle ODA={\mathrm{90°}}^{}]\end{array}$

In $\Delta OCE$

$\begin{array}{cc}O{\mathrm{C²}}^{}& =C{\mathrm{E²}}^{}+O{\mathrm{E²}}^{}\cdots \left(3\right)\\ & [\because \angle OEC={\mathrm{90°}}^{}]\end{array}$

Adding $\left(1\right),\left(2\right)$ and $\left(3\right)$

$\begin{array}{cc}& O{\mathrm{A²}}^{}+O{\mathrm{B²}}^{}+O{\mathrm{C²}}^{}\\ =\left[\begin{array}{c}A{\mathrm{F²}}^{}+O{\mathrm{F²}}^{}+B{\mathrm{D²}}^{}+O{\mathrm{D²}}^{}\\ +C{\mathrm{E²}}^{}+O{\mathrm{E²}}^{}\end{array}\right]\end{array}$

$\begin{array}{c}\\ & \left[\begin{array}{c}O{\mathrm{A²}}^{}+O{\mathrm{B²}}^{}+O{\mathrm{C²}}^{}-O{\mathrm{D²}}^{}\\ -O{\mathrm{E²}}^{}-O{\mathrm{F²}}^{}\end{array}\right]\end{array}$= AF²+BD²+CE²⋯(4)

(ii) From $\left(4\right)$

[OA²+OB²+OC²−OD²−OE²−OF²] = AF²+BD²+CE²⋯(4)

$$\begin{array}{cc}& \left[\begin{array}{c}(O{\mathrm{A²}}^{}-O{\mathrm{E²}}^{})+(O{\mathrm{B²}}^{}-O{\mathrm{F²}}^{})\\ +(O{\mathrm{C²}}^{}-O{\mathrm{D²}}^{})\end{array}\right]\\ & =A\mathrm{F²}+B{\mathrm{D²}}^{}+C{\mathrm{E²}}^{}\end{array}$$

$$\begin{array}{c}\\ & \text{(Rearranging the left side terms)}\end{array}$$

$$\begin{array}{cc}& A\mathrm{E²}+B{\mathrm{F²}}^{}+C{\mathrm{D²}}^{}\\ =A\mathrm{F²}+B{\mathrm{D²}}^{}+C{\mathrm{E²}}^{}\end{array}$$

[$\because \Delta OAE,\Delta OB\mathrm{D\; and}$ $\Delta OCE$ are right triangles]

Q. 9. A ladder 10 m long reaches a window 8 m above the ground. ind the distance of the foot of the ladder from base of the wall.
Solution:

$\mathrm{Given\; :}$

AB is height of the windows from the ground $=8m$

$AC$ is the length of the ladder $=10m$

$\mathrm{Let\; in\; the\; figure,}$

BC is the distance between foot and the ladder $=\; a$

Dince $\Delta ABC$ is right angled triangle $(\angle ABC={\mathrm{90°}}^{})$

$$\begin{array}{cc}B{\mathrm{C²}}^{}& =A{\mathrm{C²}}^{}-A{\mathrm{B²}}^{}\end{array}$$[Pythagoras  Theorem]

BC²=10²−8²

BC²=100−64

BC² =36

BC=6m

The distance between foot of wall and the ladder is $=6m$

Q. 10. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution:

Given:

 The length of the pole AB =18m

 The length of the guy wire AC =24m

Distance between stake & pole = BC

In $\Delta ABC$

$\angle ABC={\mathrm{90°}}^{}$

$$\begin{array}{cc}B{\mathrm{C²}}^{}& =A{\mathrm{C²}}^{}-A{\mathrm{B²}}^{}\\ & \left[\text{Pythagoras}\text{Theorem}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ B{\mathrm{C²}}^{}& ={\mathrm{24²}}^{}-{\mathrm{18²}}^{}\end{array}$$

$$\begin{array}{c}BC²=576-324\end{array}$$

$$\begin{array}{c}BC²=252\end{array}$$

$$\begin{array}{c}BC=6\sqrt{7}\end{array}$$

Q. 11. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 112 hours?
Solution:

$A$ is the distance travelled towards north 

AB =1000km/hr×1½hr

AB = 1000×3/2km

AB = 1500km

The distance travelled by another aeroplane towards south

$$\begin{array}{cc}BC& =1200\text{km/hr}\times \mathrm{1½}\text{hr}\end{array}$$

$$\begin{array}{c}\\ & BC\; =1200\times \frac{\mathrm{3/}}{2}\end{array}$$

$$BC\; =1800\text{km}$$

Now, In $\Delta ABC,\angle ABC={\mathrm{90°}}^{}$

$$\begin{array}{cc}A\mathrm{C²}& =A{\mathrm{B²}}^{}+B{\mathrm{C²}}^{}\\ \left[\text{Pythagoras T}\text{heorem}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ & AC²\; ={(1500)²}^{}+{(1800)²}^{}\end{array}$$

$$\begin{array}{c}AC² =2250000+3240000\end{array}$$

$$\begin{array}{c}AC² =5490000\end{array}$$

$$\begin{array}{c}AC\; =\sqrt{549000}\end{array}$$

$$\begin{array}{c}\\ & AC\; =300\sqrt{61}\text{km}\end{array}$$

The distance between two planes after  $\mathrm{1½}\text{hr}=300\sqrt{61}\text{km}$

Q. 12. Two poles of heights 6 m and 11m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution:

 The height of one pole AB $=6m$

 The height of another pole CD $=11m$

 Distance between poles bottom AC =12m

Distancebetween the tops of the poles BD =?

Draw $BE\parallel \; AC$

Now consider,

In $\Delta BED$

$$\begin{array}{cc}\angle BED& ={\mathrm{90°}}^{}\end{array}$$

$$\begin{array}{cc}BE\; =AC& =12m\end{array}$$

$$\begin{array}{c}DE\; =CD-CE\end{array}$$

$$\begin{array}{c}DE\; =11-6\end{array}$$

$$\begin{array}{c}\mathrm{DE}=5cm\end{array}$$

Now,

$$\begin{array}{cc}B{\mathrm{D²}}^{}& =B{\mathrm{E²}}^{}+D{\mathrm{E²}}^{}\\ \left[\text{Pythagoras}\text{Theorem}\right]\end{array}$$

$$\begin{array}{c}\\ & \\ & BD²\; ={\mathrm{12²}}^{}+{\mathrm{5²}}^{}\end{array}$$

$$\begin{array}{c}\\ & BD²\; =144+25\end{array}$$

$$\begin{array}{c}BD²\; =169\end{array}$$

$$\begin{array}{c}BD\; =13m\end{array}$$

The distance between the tops of poles $=13m$

Q. 13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².

Solution:

Steps:

Given: In $\Delta ABC,\angle ABC={90}^{\circ }$

$D$, $E$ are points on $AC$ and $BC$

Construction:

Join $AE$, $DE$ and $BD$

 Proof:

In $\Delta ACE$ ,

$$\begin{array}{cc}A\mathrm{E²}& =A{\mathrm{C²}}^{}+C{\mathrm{E²}}^{}\dots \left(1\right)\\ & \left[\text{Pythagoras}\text{Theorem}\right]\end{array}$$

In $\Delta DCB$

$$\begin{array}{c}B\mathrm{D²}=C{\mathrm{D²}}^{}+B{\mathrm{C²}}^{}\dots \left(2\right)\end{array}$$

Adding $\left(1\right)$ and $\left(2\right)$

$$\begin{array}{cc}& A\mathrm{E²}+B{\mathrm{D²}}^{}\\ =A{\mathrm{C²}}^{}+C\mathrm{E²}+C{D}^{\mathrm{²}}+B{\mathrm{C²}}^{}\end{array}$$

$$\begin{array}{c}\\ & =A{\mathrm{C²}}^{}+B\mathrm{C²}+E{\mathrm{C²}}^{}+C{\mathrm{D²}}^{}\end{array}$$

$$\begin{array}{c}\\ & =A{\mathrm{B²}}^{}+D\mathrm{E²}\end{array}$$

$$\begin{array}{cc}& \text{In}\Delta ABC,\angle C={90}^{\circ }\end{array}$$

$$\begin{array}{c}\\ & \Rightarrow A{\mathrm{C²}}^{}+B\mathrm{C²}=A{\mathrm{B²}}^{}\end{array}$$

Q. 13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2.

Solution:



Steps:

Given: In $\Delta ABC,\angle ABC={90}^{\circ }$

$D$, $E$ are points on $AC$ and $BC$

Construction:

Join $AE$, $DE$ and $BD$

 Proof:

In $\Delta ACE$ ,

$$\begin{array}{cc}A\mathrm{E²}& =A{\mathrm{C²}}^{}+C{\mathrm{E²}}^{}\dots \left(1\right)\\ & \left[\text{Pythagoras}\text{Theorem}\right]\end{array}$$

In $\Delta DCB$

$$\begin{array}{c}B\mathrm{D²}=C{\mathrm{D²}}^{}+B{\mathrm{C²}}^{}\dots \left(2\right)\end{array}$$

$$\text{In}\Delta ABC,\angle C={90}^{\circ }$$

$$\begin{array}{c}\\ & \Rightarrow AB²\; =A{\mathrm{C²}}^{}+B\mathrm{C²\; .....(3)}\end{array}$$

Adding $\left(1\right)$ and $\left(2\right)$

$$\begin{array}{cc}& A\mathrm{E²}+B{\mathrm{D²}}^{}\\ =A{\mathrm{C²}}^{}+C\mathrm{E²}+C{D}^{\mathrm{²}}+B{\mathrm{C²}}^{}\end{array}$$

$$\begin{array}{c}\\ & =A{\mathrm{C²}}^{}+B\mathrm{C²}+E{\mathrm{C²}}^{}+C{\mathrm{D²}}^{}\end{array}$$

$$\begin{array}{c}\\ & =A{\mathrm{B²}}^{}+D\mathrm{E²}\end{array}$$

= AB² + DE²

Q. 14 The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3CD (see the figure). Prove that 2AB² = 2AC² + BC².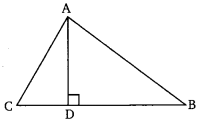

Solution:

Given: In $\Delta ABC$

$AD\perp BC$ and $BD=3CD$

$$\begin{array}{cc}BD+CD& =BC\end{array}$$

$$\begin{array}{c}\\ 3CD+CD& =BC\end{array}$$

$$\begin{array}{c}\\ 4CD& =BC\end{array}$$

$$\begin{array}{c}\\ CD& =\frac{\mathrm{1/}}{4}BC\dots \left(1\right)\end{array}$$

$$\begin{array}{c}\\ & \\ & and\end{array}$$

$$\begin{array}{c}\\ & \\ BD& =\frac{\mathrm{3/}}{4}BC\dots \left(2\right)\end{array}$$

In RA $\Delta ADC$,

$$\begin{array}{cc}A{\mathrm{C²}}^{}& =A\mathrm{D²}+C{\mathrm{D²}}^{}\\ \left[\angle ADC={\mathrm{90°}}^{}\right]\end{array}$$

$$\begin{array}{c}\\ A{\mathrm{D²}}^{}& =A{\mathrm{C²}}^{}-C{\mathrm{D²}}^{}\dots .\left(3\right)\end{array}$$

In RA $\Delta ADB$,

$$\begin{array}{cc}A{\mathrm{B²}}^{}& =A\mathrm{D²}+B{\mathrm{D²}}^{}\\ \left[\angle ADB={\mathrm{90°}}^{}\right]\end{array}$$

$$\begin{array}{c}\\ A{\mathrm{B²}}^{}& =A{\mathrm{C²}}^{}-C{\mathrm{D²}}^{}+B{\mathrm{D²}}^{}\\ \left[from\left(3\right)\right]\end{array}$$

$$\begin{array}{c}\\ A{\mathrm{B²}}^{}& =A{\mathrm{C²}}^{}+{(\frac{\mathrm{3/}}{4}BC)²}^{}-{(\frac{\mathrm{1/}}{4}BC)²}^{}\end{array}$$

$$\begin{array}{c}\\ & \left[from\left(1\right)and\left(2\right)\right]\end{array}$$

$$\begin{array}{c}\\ & \\ A{\mathrm{B²}}^{}& =A{\mathrm{C²}}^{}+\; (\frac{9B{\mathrm{C²}}^{}-B{\mathrm{C²)/}}^{}}{}\end{array}$$16

AB²=AC²+8BC²/16AB²

       =AC²+½BC²

2AB²=2AC²+BC²

Q. 15. In an equilateral triangle ABC, D is a point on side BC, such that BD = 13BC. Prove that 9AD² = 7AB².
Solution:

Steps:

$\begin{array}{c}\text{Given: In ΔABC};\end{array}$

$\begin{array}{cc}& AB=BC=CA\\ & \text{and}BD=\frac{\mathrm{1/}}{3}BC\end{array}$

$\begin{array}{c}\\ & \text{Draw}AE\perp B\mathrm{C\; BE}\\ =CE=\frac{\mathrm{1/}}{2}BC\end{array}$

[ $\because$ In an equilateral triangle perpendicular drawn from vertex to opposite side bisects the side]

Now In $\Delta ADE$

$\begin{array}{cc}A{\mathrm{D²}}^{}& =A\mathrm{E²}+D{\mathrm{E²}}^{}\\ & \left[\text{Pythagoras Theorem}\right]\end{array}$

$\begin{array}{c}=\frac{\sqrt{\mathrm{3/}}}{\mathrm{2(BC}})+{(BE-BD)²}^{}\end{array}$

[ $\because \; AE$ is the height of an equilateral triangle which is equal to $\begin{array}{c}\frac{\sqrt{\mathrm{3/}}}{2}\end{array}$ side]

$$\begin{array}{cc}A{\mathrm{D²}}^{}& =\frac{\mathrm{3/}}{4}B{\mathrm{C²}}^{}+{[\frac{B\mathrm{C/2}}{}-\frac{B\mathrm{C/}}{3}]²}^{}\end{array}$$

$$\begin{array}{c}AD²=\frac{\mathrm{3/}}{4}B{\mathrm{C²}}^{}+{(\frac{B\mathrm{C/}}{6})²}^{}\end{array}$$

$$\begin{array}{c}AD²=\frac{\mathrm{3/}}{4}B{\mathrm{C²}}^{}+\frac{B{\mathrm{C²/}}^{}}{36}\end{array}$$

$$\begin{array}{c}AD²=(\frac{27B{\mathrm{C²}}^{}+B{\mathrm{C²}}^{}}{\mathrm{)/}}\\ 36\end{array}$$

$$\begin{array}{c}AD²=28B{\mathrm{C²/36}}^{}\end{array}$$

$$\begin{array}{c}\\ 9A{\mathrm{D²}}^{}& =7B{\mathrm{C²}}^{}\end{array}$$

$$\begin{array}{c}\\ 9A{\mathrm{D²}}^{}& =7A{\mathrm{B²}}^{}\\ & \left[AB=BC=CA\right]\end{array}$$

Q. 16 In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:

In $\Delta ABC$

$AB=BC=CA$

$\begin{array}{cc}& AD\perp BC\\ \Rightarrow & BD=CD=\frac{B\mathrm{C/}}{2}\end{array}$ 

Now In $\Delta ADC$

$$\begin{array}{cc}& A{\mathrm{C²}}^{}=A{\mathrm{D²}}^{}+C{\mathrm{D²}}^{}\end{array}$$

$$\begin{array}{c}BC2=A{\mathrm{D²}}^{\mathrm{+}}{(\frac{B\mathrm{C/}}{2})²}^{}\\ & [AC=BC\mathrm{and}CD=\frac{B\mathrm{C/}}{2}]\end{array}$$

$$\begin{array}{c}\\ & B{\mathrm{C²}}^{}=A{\mathrm{D²}}^{}+\frac{B{\mathrm{C²/}}^{}}{4}\end{array}$$

$$\begin{array}{c}\frac{}{}\\ & B{\mathrm{C²}}^{}-\frac{B{\mathrm{C²/}}^{}}{4}=A{\mathrm{D²}}^{}\end{array}$$

$$\begin{array}{c}\\ & \frac{3B{\mathrm{C²/}}^{}}{4}=A{\mathrm{D²}}^{}\end{array}$$

$$\begin{array}{c}3BC²=4A{\mathrm{D²}}^{}\end{array}$$

Chapter 6 Ex.6.5 Question 17

Q. 17 Tick the correct answer and justify : In $\Delta ABC$, $AB=$ $6\sqrt{3}\text{cm}$ , $AC=$ $12cm$ and $BC=$ $6cm$. The angle $B$ is

(A) ${120}^{\circ }$

(B) ${60}^{\circ }$

(C) ${90}^{\circ }$

(D) ${45}^{\circ }$

Solution ( c)

In $\Delta ABC$

$$\begin{array}{cc}AB& =6\sqrt{3}cm;\end{array}$$

$$\begin{array}{c}\\ AC& =12cm;\end{array}$$

$$\begin{array}{c}\\ BC& =6cm\end{array}$$

$$\begin{array}{c}\mathrm{Checking\; by\; Pythagorean\; Theorem}\end{array}$$

$$\begin{array}{c}AC²\; =\; AB²+B{\mathrm{C²}}^{}\end{array}$$

$$\begin{array}{c}{\mathrm{(12)²\; =\; (6\surd 3)²+(6)²}}^{}\end{array}$$

$$\begin{array}{cc}{}^{}& 108+36\end{array}$$

$$\begin{array}{c}144\; =144\end{array}$$

$$\begin{array}{c}\\ \Rightarrow A{\mathrm{C²}}^{}& =A{\mathrm{B²}}^{}+B{\mathrm{C²}}^{}\end{array}$$

Pythagoras theorem is satisfied

$$\Rightarrow \angle ABC={\mathrm{90°}}^{}$$