Trigonometry
Trigonometry is the study of relationships between the sides and angles of a right-angled triangle.
Question 1.
In ∆ABC right angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution:
by Pythagorean Theorem
H² = P² + B²
= (24)² + (7)²
= 576 +49
H² = 25²
H= 25
Question 2.
In given figure, find tan P – cot R.
Solution:
by Pythagorean Theorem
Question 3.
If sin A =
Solution:
Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:
Question 5.
Given sec θ =
Solution:
We know that
sec θ = 13/12
AB/AC =
Let AC = 13k and AB = 12k
by the Pythagorean Theorem
AC² = AB² + BC²
BC² = AC² – AB² = (13k)² –(12k)²
= 169k² – 144k² = 25k²
BC² = 25k²
BC = 5k
Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:
Angle opposite to equal sides are equal.
Question 7.
If cot θ =
(i) [
(ii) cot²θ
Solution:
cot θ = 7/8
AB/BC = 7/8
let AB = 7k and BC =8k
then in ∆ABC
AC² = AB² + BC²
= (7k)² + (8k)²
= 49k² + 64k² = 113k²
AC² = 113k²
AC = k√113
Question 8.
If 3 cot A = 4, check whether (
Solution:
do yourself
Q. 9.I Intriangle ABC, right angled at B, if tan A =
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:
We know that
tan θ = 1/√3
BC/AB = 1/√3
let BC = 1k and AB =√3k
then in ∆ABC
AC² = AB² + BC²
= (√3k)² + (1k)²
= 3k² + 1k² = 4k²
AC² = 4k²
AC = 2k
(i) sin A cos C + cos A sin C(ii) cos A cos C – sin A sin C
Question 10.
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:
We know that
PR + QR = 25 cm
PQ = 5 cm.
Let QR = x
then PR = 25 – x
by the Pythagorean Theorem
PR² = PQ² + QR²
PQ² = PR² – QR²
(5)² = (25–x )² – (x)²
25 = (25)² + (x)² – 2×25×x –(x)²
25 = 625 + x² – 50x –x²
25 = 625 – 50x
50x = 625–25
50x = 600
x= 600/50=12
Now PR = 25 – 12
PR = 13
Question 11.
State whether the following statements are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A =
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ =
Solution:
(i) False
the value depends on the sides of the triangle so then we may have any value.
(ii) True
Because sec A is always greater than 1
(iii) False
cos A is the abbreviation used for the cosine of angle A.
(iv) False
cot A is not the product of cot and A it is single cot A.
(v) False
The value of sin theta cannot be less than 1
Exercise 8.2
Note:– The values of the trigonometric ratios of an angle do not vary with the lengths of the sides of the triangle, if the angle remains same.
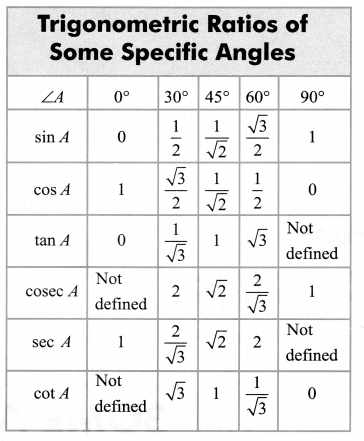
Question 1.
Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2tan²45°+ cos²30°– sin²30°
(iii)
cos 45°
sec 30° + cosec 30°
(iv)
sin 30° + tan 45°– cosec 60° sec 30° + cos 60° + cot 45°
(iv)
5cos²30° + 4sec30°– tan45° sin²30° + cos²60°
Solution:
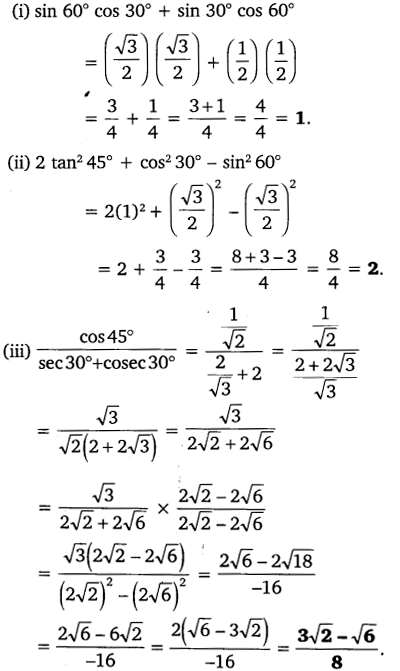
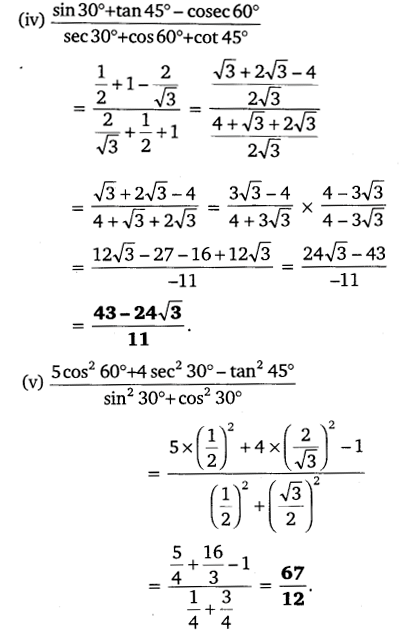
Question 2.
Choose the correct option and justify your choice:
2 tan30°/(1+tan² 30°)
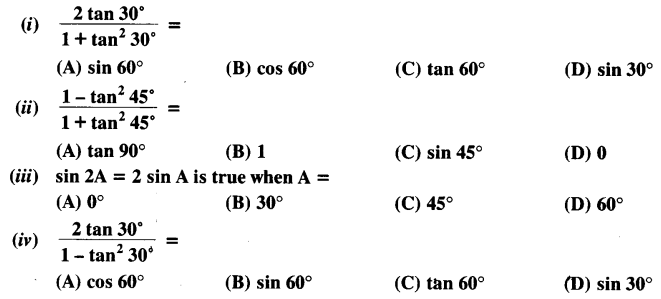
Solution:

Ex 8.2 Class 10 Maths Question 3.
If tan (A + B) = √3 and tan (A – B) = 1√3 ; 0° < A + B ≤ 90°; A > B, find A and B.
Solution:
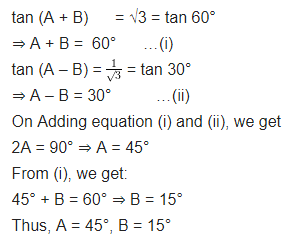
Question 4.
State whether the following statements are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution:
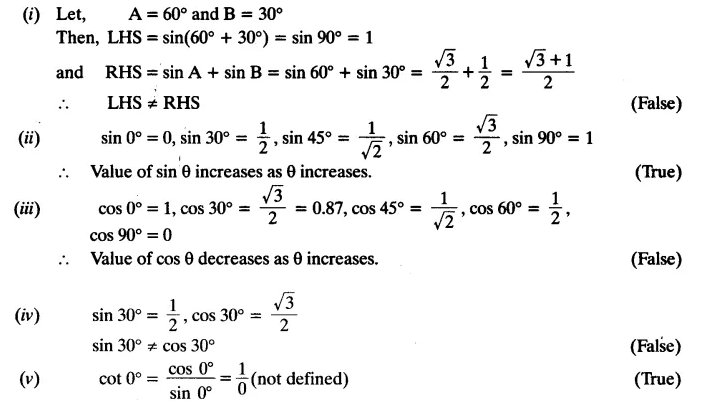

Question 1.
Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2tan²45°+ cos²30°– sin²30°
(iii)
cos 45°
sec 30° + cosec 30°
(iv)
sin 30° + tan 45°– cosec 60° sec 30° + cos 60° + cot 45°
(iv)
5cos²30° + 4sec30°– tan45° sin²30° + cos²60°
Solution: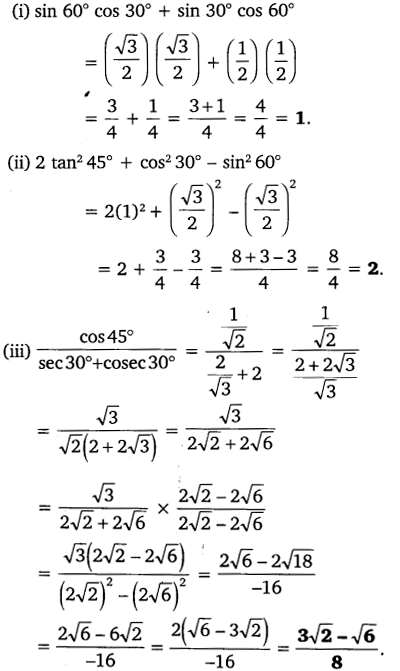
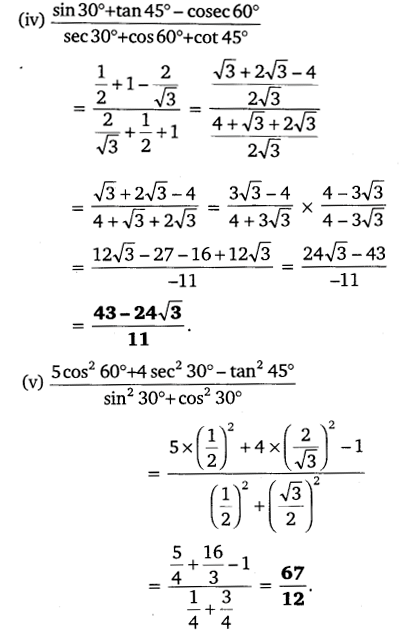
Question 2.
Choose the correct option and justify your choice:
2 tan30°/(1+tan² 30°)
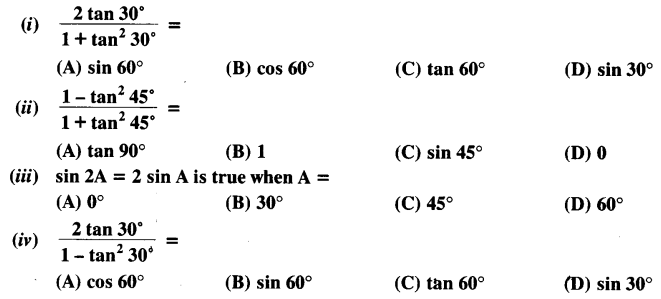
Solution:
Question 3.
If tan (A + B) = √3 and tan (A – B) =
Solution: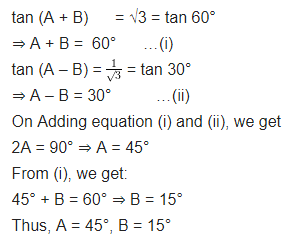
Question 4.
State whether the following statements are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution: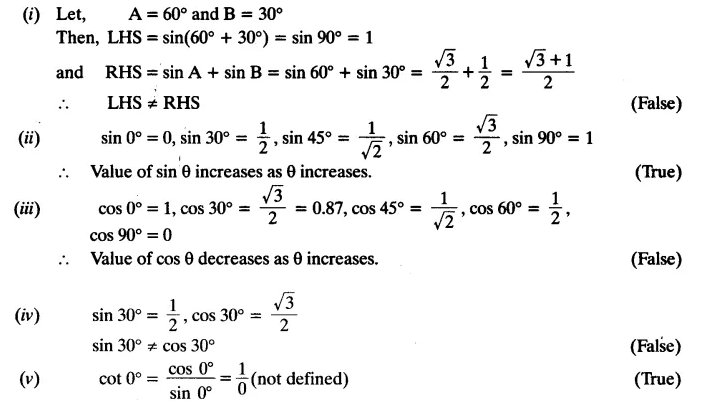
Ex 8.3
Ex 8.3
Trigonometric Ratios for Complementary Angles
sin (90° – A) = cos A
cos (90° – A) = sin A
tan (90° – A) = cot A
cot (90° – A) = tan A
sec (90° – A) = cosec A
cosec (90° – A) = sec A
Note:
Here (90° – A) is the complementary angle of A.
sin (90° – A) = cos A
cos (90° – A) = sin A
tan (90° – A) = cot A
cot (90° – A) = tan A
sec (90° – A) = cosec A
cosec (90° – A) = sec A
Note:
Here (90° – A) is the complementary angle of A.
Question 1.
Evaluate:

Solution:
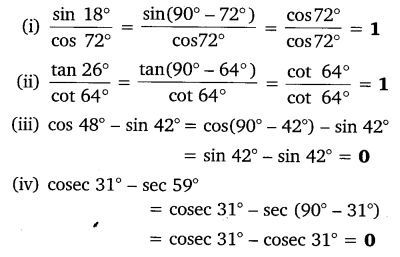
Question 2.
Show that:
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:

Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution:
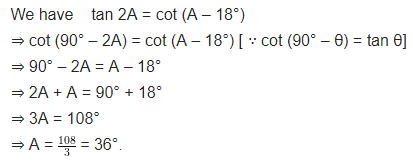
Question 4.
If tan A = cot B, prove that A + B = 90°.
Solution:
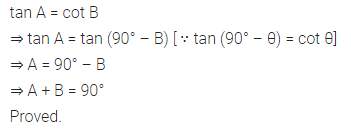
Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:
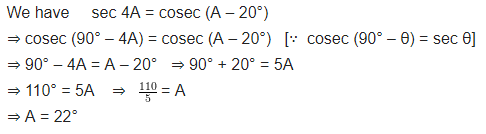
Question 6.
If A, B and C are interior angles of a triangle ABC, then show that: sin (B+C2 ) = cos A2
Solution:
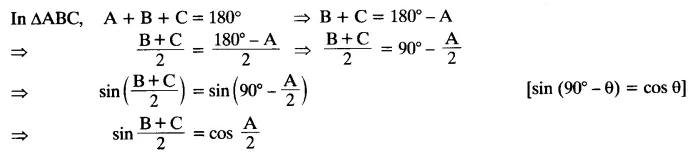
Question 7.
Express sin 61° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
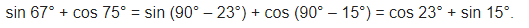
Question 1.
Evaluate:![]()
Solution: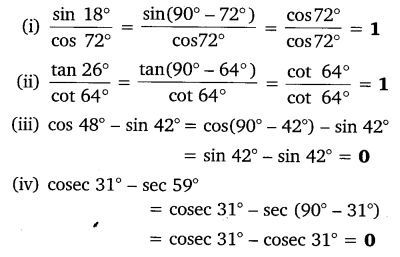
Question 2.
Show that:
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:
Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution: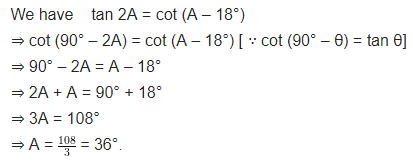
Question 4.
If tan A = cot B, prove that A + B = 90°.
Solution: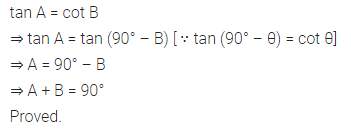
Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution: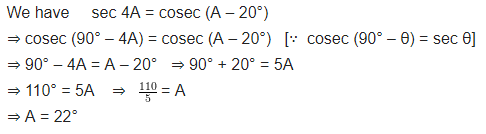
Question 6.
If A, B and C are interior angles of a triangle ABC, then show that: sin (
Solution: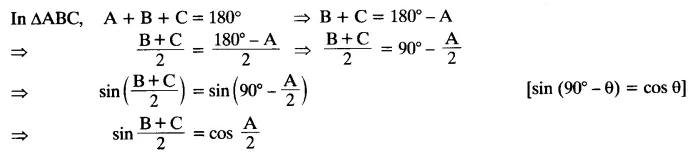
Question 7.
Express sin 61° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:![]()
Ex 8.4
Trigonometric Identities
An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle(s) involved.[for 0° ≤ θ ≤ 90°]
(i) sin2θ + cos2θ = 1
(ii) sec2θ – tan2θ = 1
An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle(s) involved.[for 0° ≤ θ ≤ 90°]
(i) sin2θ + cos2θ = 1
(ii) sec2θ – tan2θ = 1
(iii) cosec2θ – cot2θ = 1
Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.Solution:

Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
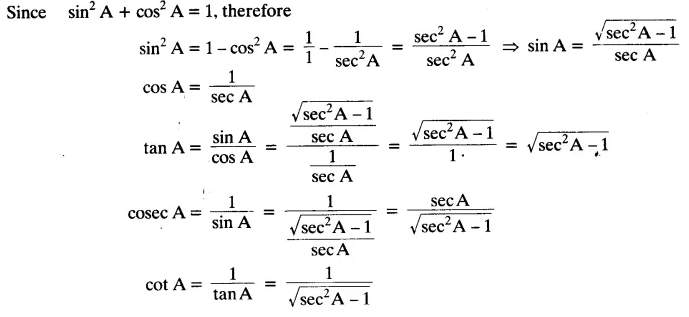
Question 3.Evaluate:
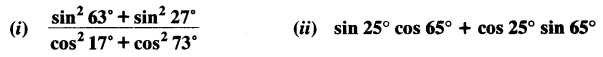
Solution:
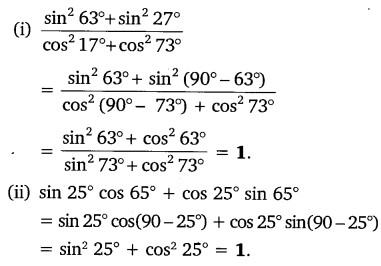
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A = ……
(A) 1 (B) 9 (C) 8 (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) = ………..
(A) 0 (B) 1 (C) 2 (D) -1
(iii) (sec A + tan A) (1 – sin A) = ………….
(A) sec A (B) sin A
(C) cosec A (D) cos A
(iv) (1+tan²A)/(1+cot²A) = ……
(A) sec² A (B) -1
(C) cot² A (D) tan² A
Solution:

Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
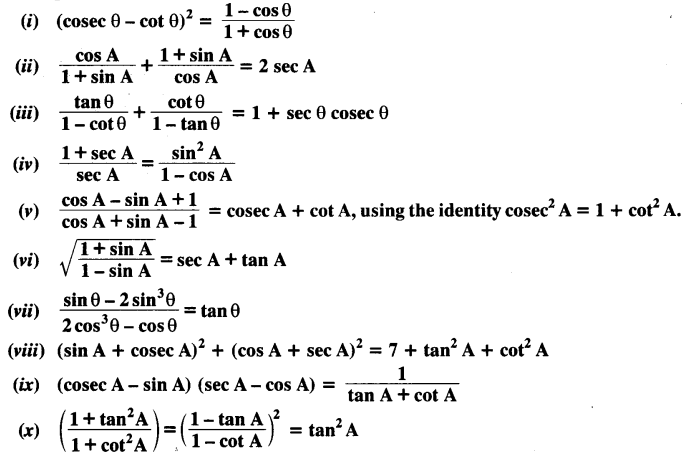
Solution:

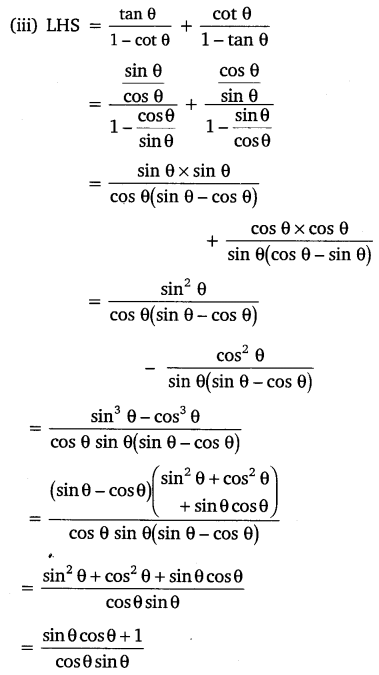

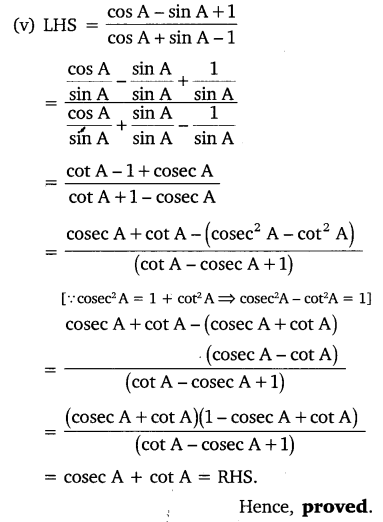


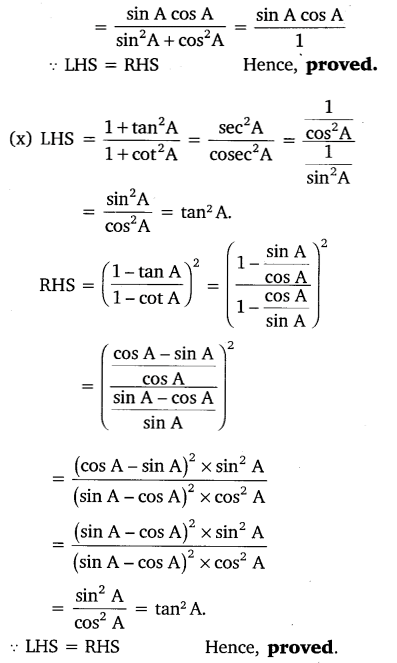
(iii) cosec2θ – cot2θ = 1
Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.Solution:

Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
Evaluate: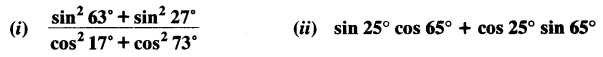
Solution: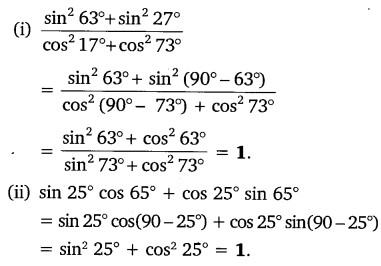
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A = ……
(A) 1 (B) 9 (C) 8 (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) = ………..
(A) 0 (B) 1 (C) 2 (D) -1
(iii) (sec A + tan A) (1 – sin A) = ………….
(A) sec A (B) sin A
(C) cosec A (D) cos A
(iv) (
(A) sec² A (B) -1
(C) cot² A (D) tan² A
Solution:
Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.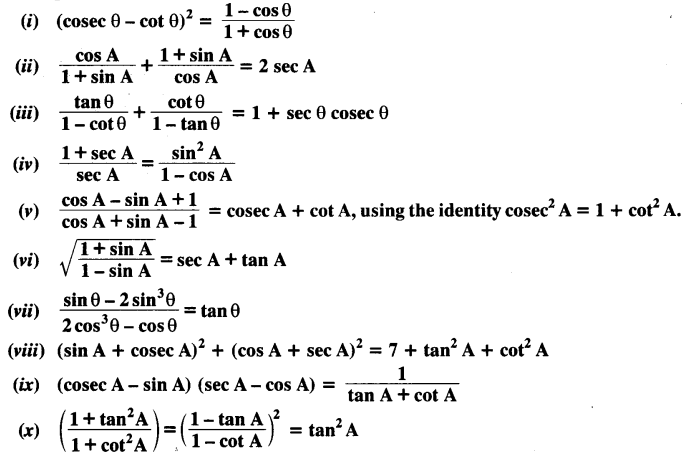
Solution:
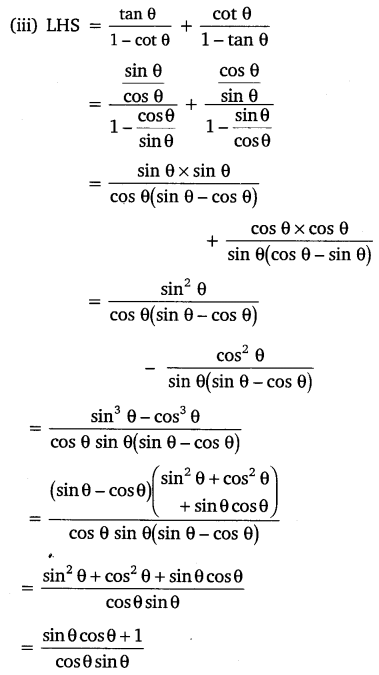

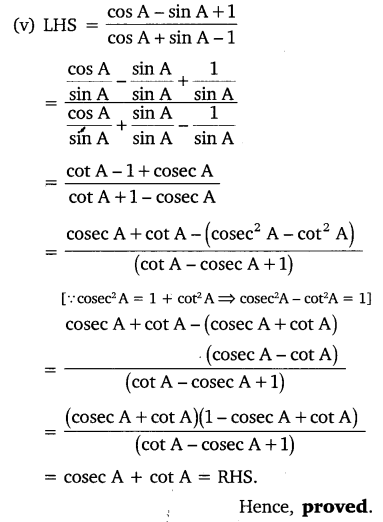



























Post a Comment
Post a Comment