Chap 8 : Motion
Quick Revision
Origan / Reference Point:- Any fixed point is called a origan or reference point, any station or bus stop is the example of the reference points.
Rest : A body is said to be in a state of rest when its position does not
change with respect to a reference point.
***** Rahul Tuition Centre *****
MOTION
Motion: A body is said to be in a state of motion when its position change continuously with reference to a point.
Motion can be of different types depending upon the type of path by which the object is going through.
Motion According To The Speed
(i) Uniform Motion – covers the same distance in equal intervals of time
(ii) Non-uniform Motion – covers the unequal distance in equal intervals of time
(a) accelerated (increased) :-
(b) Deaccelerated / retardation (decreased) :-
(A) Motion According To The Speed Paath
(i) Circulatory motion/Circular motion – In a circular path.
(ii) Linear /Rectilinear motion – In a straight line path.
(iii) Oscillatory / Vibratory motion – To and fro path with respect to origin.
***** Rahul Tuition Centre *****
QUANTITY
Scalar Quantity: Quantity with magnitude – As distance, length, mass, time, area, volume, work, power, energy, temperature, speed, pressure, charge etc.
Vector Quantity: Quantity with magnitude and direction –as displacement, Weight, Velocity etc.
***** Rahul Tuition Centre *****
Distance:- The path covered by a body between initial and final position is called distance. It is scalar quantity. Its unit is also meter (m).
Displacement :- The shortest distance between the initial and final position is called displacement. It is vector quantity. And its unit is m (Meter).
Zero Displacement :- When the final and initial stage is same the displacement will be zero.
Difference between Distance and Displacement
***** Rahul Tuition Centre *****
Speed: The distance traveled by the body in per unit time is called
speed.
Distance
Speed = _________
Time
SI unit of speed is meter per second or m/s or ms–¹.
It is scalar quantity.
Odometer Of An Automobile :- The odometer of an automobile measures the distance covered by an automobile.
Average Speed: The average distance covered by a moving body in unit time is called average speed of body.
SI unit of speed is
meter per second or
m/s or
ms–¹.
***** Rahul Tuition Centre *****
Velocity: The distance traveled by a moving body (displacement) in per unit time in a given direction is called velocity
SI unit of Velocity is the same to speed as meter per second or m/s or ms–¹.
It is vector quantity.
Initial Velocity :- Velocity at it will start, it is denoted by 'u'.
Final Velocity:- Velocity at it will end, it is denoted by 'v'.
Change In Velocity:- Distance between final and initial velocity is known as changing in velocity.
Positive (+) Velocity :- When velocity is increasing.
Negative (–) Velocity :- When velocity is decreasing.
Zero (0) Velocity:- When object is moving in uniform velocity
Difference Between Speed And Velocity
Uniform (Constant) Velocity:- If a body travels in a straight line and covers equal distance in equal
intervals of time is called uniform velocity.
Angular Velocity:- The rate of change of angular displacement is called angular velocity.
Average Velocity :- The arithmetic mean of initial and final velocity for a given period of time is called Average Velocity.
***** Rahul Tuition Centre *****
Acceleration: The ration of change of velocity with time of a moving object is called acceleration.
SI unit of acceleration is m/s²
or ms–².
Positive (+) Acceleration :- Acceleration is Positive (+) if v > u or in the direction of the velocity or velocity is increasing.
Negative (–) Acceleration:-
Acceleration is Negative (–) if v < u or in the opposite direction of the velocity or velocity is decreasing.
Zero (0) Acceleration :- If v = u or body is moving in a uniform velocity
Retardation (deceleration) Or negative Acceleration:- A body is said to be retarded if its velocity is decreasing or slow downing the body.
Negative acceleration (if velocity is decreasing) is called retardation or
deceleration.
***** Rahul Tuition Centre *****
Speed = Distance / time
velocity = Displacement / time
Average Velocity =
EQUATION OF MOTION
(i) v = u + at
(ii) s = ut + 1/2. at²
(iii) v² = u² + 2as
***** Rahul Tuition Centre *****
Ans. (b) non-uniform
43. The numerical ratio of displacement to distance for a moving object is
(a) always less than 1
(b) always equal to 1
(c) always more than 1
(d) equal or less than 1
Ans. (d) equal or less than 1
44. If the displacement of an object is proportional to square of time, then the object moves with
(a) uniform velocity
(b) uniform acceleration
(c) increasing acceleration
(d) decreasing acceleration
Ans. (b) uniform acceleration
45. Fill in the blanks:
The slope of velocity-time graph gives …………….. and the slope of displacement-time graph gives ……………..
Ans. acceleration, velocity
46. From the given υ – t graph, it can be inferred that the object is
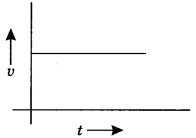
(a) in uniform motion
(b) at rest
(c) in non-uniform motion
(d) moving with uniform acceleration
Ans. (a) in uniform motion
47. Four cars A, B, C and D are moving on a levelled road. Their distance versus time graphs are shown in the adjacent figure. Choose the correct statement.
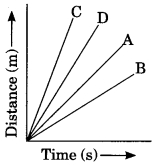
(a) Car A is faster than car D.
(b) Car B is the slowest.
(c) Car D is faster than car C.
(d) Car C is the slowest.
Ans. (b) Car B is the slowest.
48. Which of the following figures correctly represents uniform motion of a moving object?
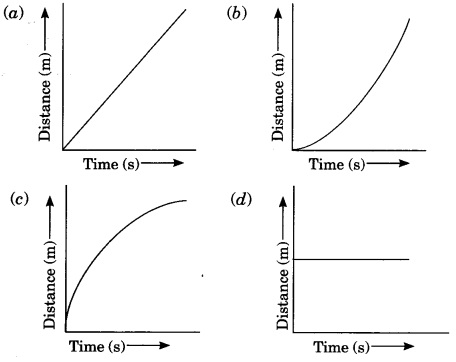
Ans. (a)
49. Velocity-time graph of an object is given below. The object has
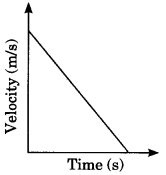
(a) Uniform velocity
(b) Uniform speed
(c) Uniform retardation
(d) Variable acceleration
Ans. (c) Uniform retardation
50. Which one of the following graphs shows the object to be stationary?
Ans. (b)
51. According to the given velocity-time graph, the object
(a) is moving with uniform velocity
(b) has some initial velocity
(c) is moving uniformly with some initial velocity
(d) is at rest
Ans. (b) has some initial velocity
52. A car is moving along a straight road with uniform velocity. It is shown in the graph.
Ans. (d)
53. Which of the following graphs is not possible?
Ans. (b)
ONE MARKS QUESTIONS
Q. 1. Define the term velocity. What is its unit? Is it a scalar or vector quantity?
Ans :
Velocity is a physical quantity that gives the speed and direction of motion of the body
Velocity = Displacement / Time
The S.I. unit of velocity is m/s or ms–¹.
Velocity is a vector quantity because its description requires both
magnitude and direction.
Q. 2. What is the relationship between distance travelled and the time elapsed for the motion with uniform velocity?
Ans :
Distance is directly proportional to time used.
In fact, distance travelled
= Uniform velocity × Time used.
Q. 3. Define acceleration. Is it a scalar or a vector quantity?
Ans :
In non-uniform motion, the velocity of a body changes with time. It has different velocities at different
instants of time and at different points of its path. In such a situation, we define a physical quantity called
acceleration which is a measure of the change in the velocity of a body per unit time. It is a vector quantity.
Q. 4. What is the Si unit of acceleration?
Ans :
The SI unit of acceleration is m/s².
Q. 5. What is the acceleration of a body moving uniform velocity?
Ans :
The acceleration of a body moving with uniform velocity is zero.
Q. 6. Differentiate acceleration from velocity.
Ans :
Velocity is the change in position of a body per unit time in a given direction and acceleration is the change in velocity of a body per unit time.
Q. 7. “The direction in which an object moves is given by the direction of velocity of the object and not the direction of acceleration.” Give an example to justify this statement.
Ans :
When an object is thrown upward, its velocity is directed upward while its acceleration is directed downwards. Thus, the velocity determines the direction of motion.
Q. 8. When is the acceleration of a body positive?
Ans :
The acceleration of a body is taken to be positive if it is in the direction of velocity.
Q. 9. Name the different types of graph.
Ans :
Bar graphs, straight line graphs, histograms, etc.
Q. 10. Which type of graph is used to describe motion?
Ans :
Line graph are used to describe the motion of an object.
Q. 11. Name the two types of physical quantities.
Ans :
The two types of physical quantities are scalar quantity and vector quantity.
Q. 12. What is magnitude?
Ans :
The numerical value of a physical quantity is called its magnitude.
Q. 13. Define a scalar quantity.
Ans :
A physical quantity which has only magnitude and no direction is called a scalar quantity.
Q. 14. Give two examples of a scalar quantity.
Ans :
Two examples of a scalar quantity are distance and speed.
Q. 15. Define vector quantity.
Ans :
A physical quantity which has both magnitude and direction is called a vector quantity.
Q. 16. Give the simplest type of motion.
Ans :
The simplest type of motion is the motion along a straight line.
17. Give two examples of a vector quantity?
Ans :
Two examples of a vector quantity are displacement and velocity.
THREE MARKS QUESTIONS
Q. 18. How can we represent the change in the position of an object with time?
Ans :
The change in the position of an object with time can be represented on the distance-time graph by adopting a convenient scale of choice.
In this graph, time is taken along x-axis and distance is taken along y-axis.
Q. 19. Why is the motion in a circle at constant speed called accelerated motion?
Ans :
When a body moves along a circular path with a constant speed, its direction of motion at any point
is along the tangent to the circle at that point, this motion called accelerated motion. The direction of
motion changes as the body moves in a circle and causes a change in the velocity. Therefore, the motion
of an object along a circular path is an accelerated motion.
Q. 20. A satellite revolves round the Earth with uniform speed. Is this motion accelerated? If so, in which
direction does the acceleration act?
Ans :
The velocity of the satellite revolving around the Earth changes due to change in its direction of motion. So, the motion of satellite is an accelerated one. The acceleration is directed towards the centre of the Earth.
Q. 21. What is the difference between uniform linear motion and uniform circular motion?
Ans :
When a body is moving with a uniform speed along a straight line, its motion is called linear uniform
motion. The uniform linear motion is an accelerated motion.
When a body is moving with a constant speed along a circular path, the direction of motion of body
changes continuously with time. We know that a change in the direction of motion implies a change in velocity. Thus, uniform circular motion is an accelerated motion even though the speed of the body remains constant.
Q. 22. When is the acceleration of a body is negative?
Ans :
The acceleration of a body is taken to be negative when it is opposite to the direction of velocity.
Q. 23. Define uniform acceleration. Give one example.
Ans :
Uniform acceleration : An object has a uniform acceleration if it travels in a straight line and its velocity increases or decreases by equal amounts in equal intervals of time.
For example : The motion of a freely falling body has uniform acceleration.
Q. 24. Define non-uniform acceleration. Give one example.
Ans :
Non-uniform acceleration : An object has non-uniform acceleration if it travels in a straight line and its
velocity increases or decreases by unequal amounts in equal intervals of time.
For example : The movement of a car on a busy road has non-uniform acceleration.
Q. 25. What is the meant by retardation? Give its S.I. unit.
or
Give an example of negative acceleration.
Ans :
Retardation : When the velocity of a body decreases with time, its final velocity is less than the initial velocity, i.e. its acceleration is negative. This negative acceleration is called retardation. The S.I. unit of
retardation is ms–².
Example : When brakes are applied to a moving car, its velocity gradually decreases. Under these conditions,
the car is under retardation.
Q. 26. How does the velocity change with time in uniform rectilinear motion of an object?
Ans :
In uniform rectilinear motion of an object, the velocity is constant with time, i.e. change in velocity of the object during any time interval is zero.
Q. 27. How does the velocity change with time in non-uniform rectilinear motion of an object?
Ans :
The velocity has different values at different instant of time and at different points of its path, i.e. change in velocity of the object during any time interval is not zero.
Q. 28. What do graphs provide?
Ans :
The graphs provide a convenient method to present pictorially the basic information about a variety of
events such as motion.
Q. 29. Give an example of use of bar graph and straight graph.
Ans :
In telecast of one-day cricket match on T.V. vertical bar graphs show the run rate of a team in over.
Straight line graph helps in solving linear equation in two variables.
Q. 30. When do we say that the position of body has changed?
Ans :
If the distance, or direction, or both of a body relative to a reference point changes then we say that the position of the body has changed.
Q. 31. Classify the following as scalar and vector quantities : Mass, weight, time, temperature, volumes, velocity, speed, forces, acceleration.
Ans :
Scalar quantity
Mass, Time, Temperature, Volume, Speed
Vector quantity
Weight, Velocity, Acceleration, Forces
*Q. 32. In a long distance race, the athletes were expected to take four rounds of the track such that the line of finish was same as the track was 200 m.
(i) What is the total distance to be covered by the athletes?
(ii) What is the displacement of the athletes when they touch the finish line?
(iii) Is the motion of the athletes uniform or non-uniform?
(iv) Is the distance moved by and displacement of athletes at the end of the race equal?
Ans :
(i) Total distance covered by the athletes = perimeter × No. of rounds
= 200 × 4
= 800 m.
(ii) The line of start and the line of finish are the same so,
Displacement = Distance between Final Point and Initial Point.
= Final Point – Initial Point
= 0
(iii) The motion of the athletes is non-uniform.
(iv) The distance and displacement of an athlete at the end of the race are not equal.
Q. 33. (i) Give an example of a body which may appear to be moving for one person and stationary for the
other.
(ii) What can we tell about motion from the above example?
Ans :
(i) The man standing on the roadside observe that a bus along with its passenger is moving.
At the same time, a passenger sitting in the bus observes his fellow passenger to be at rest.
(ii) We can tell that motion is relative.
Q. 34. How many different kinds of motion are there? Name them. Is there any motion which is a combination of two or more types of motion?
Ans :
(i) There are three kinds of motion. These are :
(a) Linear or translatory motion.
(b) Circular or rotational motion.
(c) Vibratory or oscillatory motion.
(ii) Complex motion means a combination of two or more types of motions.
Q. 35. What is motion? Give some examples of directly perceivable motion in daily life.
Ans :
(i) A body is said to be in motion if it changes its position in relation to a reference point (origin).
(ii) Some examples of directly perceivable motion in daily life are :
(a) Birds and animals moving from one place to another.
(b) Cars moving on the roads.
(c) Aeroplanes flying in the sky.
(d) Blades of a moving fan.
(e) Fish swimming in water.
Q. 36. (i) Give an example of motion in human body which cannot be perceived directly.
(ii) Give an example of motion in nature which cannot be perceived directly.
(iii) Give an example of motion of the Earth which cannot be perceived directly.
Ans :
(i) The motion of blood through veins and arteries in human body cannot be perceived directly.
(ii) The motion of air is not perceived directly. We perceive it by observing the movement of dust or leaves of trees, etc.
(iii) The phenomena of sunrise, sunset and change of seasons is due to rotation and revolution of the Earth which cannot be perceived directly.
Q. 37. Define the following :
(i) Translatory motion
(ii) Complex motion
Ans :
(i) When a body moves along a straight line, its motion is called rectilinear or translatory motion.
For example : A car moving on a straight road.
(ii) When a body has two or more types of motion, it is said to possess complex motion.
For example : A ball rolling down on inclined planes has both rectilinear as well as circular motion.
Q. 38. (i) Give some examples of erratic and uncontrolled motion.
(ii) Give an example of controlled motion which can be a service to human beings.
(iii) Is there a need to study about the erratic which of some objects and learn to control them?
Ans :
(i) Flooded river, a hurricane, a tsunami, etc.
(ii) Controlled motion of a river in a dam is useful to generate hydroelectric power.
(iii) Yes, we should study about the erratic motion of some objects because it will help us in disaster
management.
NUMERICAL QUESTIONS
Q. 39. A person moves along the boundary of a square field of side 10 m in 20 s. What will be the magnitude of displacement of that person at the end of 2 minutes
20 seconds?
Ans :
Side of square field = 10 m
So, perimeter of square = 4 × Side
= 4 × 10 m
= 40 m
Person moves along the boundary in 20 sec.
Time = 2 m 20 sec
= 2 × 60 s + 20 s
= 140 s
Since in 20 s person moves = 40 m.
Therefore, in 1 sec distance covered = 40/2
= 2 m
Therefore, distance covered in 140 sec = 2 × 140
= 280 m
Now, number of rotation to cover 280 along the boundary
No. of rotation= Total distance / Perimeter
= 280 / 40
= 7 rounds.
Hence, after 7 rounds the person will be at the starting point,
Now
Displacement = Distance between Final Point and Initial Point.
= Final Point – Initial Point
= 0
Displacement will be zero.
40. Neha swims in a 90 m long pool. She covers 180 m in one minute by swimming from one end to the other
and back along the same straight path. Find the average speed and average velocity of Neha.
Ans :
Total distance = 180 m
Total displacement = 0
Time taken T = 1 min = 60 s
Average speed = Total time taken / Total distance
= 180/ 60
= 3 m/s
Average Velocity = Displacement / Total time taken
= 0/60
= 0 m/s
41. A car decreases its speed from 80 km/h to 60 km/h is 5 seconds. Find the acceleration of the car.
Ans :
u = 80 km/h
= 80 × 1000/(60 × 60)
= 80 × 5/18
= 22.22 m/s
v = 60 km/h
= 60 × 1000/(60 × 60)
= 60 × 5/18
= 16.67 m/s
Time (t) = 5 s
= –1.11 m/s²
42. A train starting from a railway station and moving with uniform acceleration, attains a speed 40 km/h in 10 minutes. Find its acceleration.
Ans :
u = 0 (starting from rest)
v = 40 km/h
= 40 km/h × 1000/(60 × 60)
= 40 km/h × 5/18
= 11.11 m/s
Time (T) = 10 minutes
= 600 s
a = 11.11 / 600
= 0.0185 m/s²
43. The average speed of a bicycle, an athlete and car are 18 km/h, 7 m/s and 2 km/min respectively. Which of the three is the fastest and which is the slowest?
Ans :
Speed of a bicycle = 18 km/h
= 18 km/h × 1000/(60 × 60)
= 18 km/h × 5/18
= 5 m/s
Speed of a athlete = 7 m/s
Speed of a car = 2 km/min
= 2 × 1000/60
= 2000/60
= 33.3 m/s
Thus, the average speeds of the bicycle, the athlete and the car are 5 m/s, 7 m/s and 33.3 m/s respectively.
So, the car is the fastest and the bicycle is the slowest.
44. Figure shows distance-time graph of two objects A and B, which object is moving with greater speed
when both are moving?
The line for object B makes a longer angle with the time-axis. Its slope is longer than the slope of the line
for object A. Thus, the speed of B is greater than thatof A.
45. Figure represents the speed time graph for a particle. Find the distance covered by the particle between t = 10 min and t = 30 min.
We draw perpendicular lines from the 10-minute point and the 30-minute point to the time-axis (fig.). The distance covered is equal to the area of the rectangle ABCD, its value is
ABCD = (30 min – 10 min) x (10 km/h)
= 20 min × 10 km/h
= 20 / 60 h × 10 km/h
= 10 /3 km
46. Find the distance covered by a particle during the time interval t = 0 to t = 20 s for which the speed-
time graph is shown in figure.
Figure: Fig. 8.35
The distance covered in the time interval 0 to 20 s is equal to the area of the shaded triangle.
So,
Area = 1/2 × base × height
=1/2 × (20 s) x (20 m/s)
= 200 m.
47. A bus moves 30 km in 30 min and the next 30 km. in 40 min. Calculate the average speed for the entire journey.
Ans :
Total time taken = 30 min + 40 min
= 70 min
= 70 / 60 h
= 7/6 h
Total distance travelled = 30 km + 30 km
= 60 km
The average speed = Total distance / Total time
= 60 km/ (7/6) h
= 360/7
= 51.4 km/h
48. A girl runs for 10 min at a uniform speed of 9 km/h. What should be the speed that she runs for the next 20 min, so that the average speed comes to 12 km/h?
Ans :
Total time = 10 min + 20 min
= 30 min
= 30/60 h
= 1/2
The average speed = 12 km/h
The average speed is 12 km/h using s = vt, the
distance covered in 30 min is
= 12 km/h × 30 min
= 12 km/h × 1/2 h
= 6 km
The distance covered in the first 10 min is :
= 9 km/h × 10 min h
= 9 km/h × 10/60 h
= 9 km/h × 1/6 h
= 9/6
= 1.5 km
Thus, he has to cover 6 km – 1.5 km = 4.5 km in the next 20 min.
Required speed = 4.5km/(20/60)h
= 4.5 × 60/20km/h
= 13.5 km/h
49. It is estimated that the radio signal takes 1.27 seconds to reach the Earth from the surface of the Moon. Calculate the distance of the Moon from the Earth. Speed of radio signal = 3 × 108 m/s (speed of light
in air).
Ans :
Here, time = 1.27 s
Speed = 3 × 108 m/s
Distance = ?
Using distance = speed × time,
we get
Distance = 3 × 108 m/s × 1.27 s
= 3.81 × 10⁸ m
= 3.81 × 10⁵ km
50. Divya walked 2 km on a straight road and then walked back 1 km. Which of the two quantities involved in her walking is greater- the scalar or vector?
Ans :
Distance travelled by Divya
= 2 km + 1 km
= 3 km
Displacement = 2 km – 1 km
= 1 km
Hence, distance which is a scalar quantity is greater than the displacement which is a vector quantity.
51. Two satellites A and B revolve around a planet C. The time taken by satellite B to go around the planet is
twice the time taken by A. Which of the two satellites will have a greater magnitude of velocity?
Ans :
Satellite A will have greater magnitude of velocity since velocity is inversely proportional to time.
v = 2π r/t
52. A child moving on a circular track of radius 40 m completes one revolution in 5 minutes. What is his
(i) average speed (ii) average velocity in one full revolution?
Ans :
Distance travelled in one revolution,
2π r =2π × 40m
Displacement in one revolution = 0
Time taken = 5 minutes
= 5 × 60s
= 300s
(i) Average speed = Distance / Time
= 2π×40/300
= 4π /15 m/s
(ii) Average velocity = Displacement / Time
= 0
























Post a Comment
Post a Comment