90.1.2 Rational Numbers Part 1.2 Pythagorean Triplets

पायथागॉरियन प्रमेय

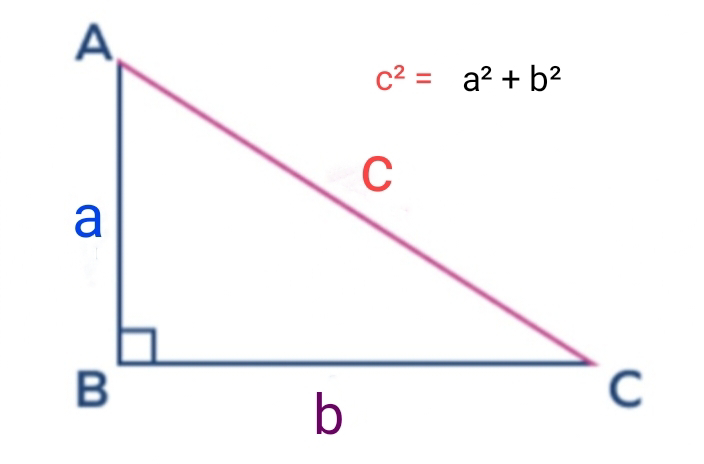
किसी भी समकोण त्रिभुज में, कर्ण का वर्ग समकोण त्रिभुज की अन्य दो भुजाओं के वर्गों के योग के बराबर होता है।

पायथागॉरियन त्रिगुणों या पायथागॉरियन त्रिक

पाइथागोरस त्रिक तीन धनात्मक पूर्णांक हैं जो पाइथागोरस प्रमेय को संतुष्ट करते हैं। 

इस प्रकार हम कह सकते हैं कि कोई भी तीन सकारात्मक पूर्णांक जो पाइथागोरस प्रमेय को पूरी तरह से संतुष्ट करते हैं उन्हें "पाइथागोरस त्रिगुण" या  "पाइथागोरस त्रिक" कहा जाता है। 

समकोण त्रिभुज

वह त्रिभुज जिसका एक कोण समकोण अर्थात 90° का होता है। समकोण त्रिभुज कहलाता है। 

इसमें तीन भुजाएं होती हैं और तीनों को ही अलग-अलग नाम से जाना जाता है।

कर्ण –> समकोण के सामने भुजा वाली भुजा को कर्ण कहते हैं। यह समकोण त्रिभुज की सबसे बड़ी भुजा होती है। इसे हम अंग्रेजी अक्षर स्मॉल सी (c) से दर्शाते हैं।

आधार –> समकोण त्रिभुज की क्षैतिज (पड़ी या लेटी) भुजा को आधार कहते हैं। इसे हम अंग्रेजी अक्षर स्मॉल ए (a) से दर्शाते हैं।

लम्ब –> समकोण त्रिभुज की उधर्वाधर (खड़ी)  भुजा को लम्ब (लंब) कहते हैं। इसे हम अंग्रेजी अक्षर स्मॉल भी (b)  से दर्शाते हैं।

क्या :(3, 4 , 5) एक पाइथागोरियन त्रिक है ?

यह 3 सकारात्मक संख्याओं का एक सेट है  यदि यह पाइथागोरस प्रमेय के सूत्र को संतुष्ट करता है तो पाइथागोरियन ट्रिक है अन्यथा नहीं।

a = 3

b = 4 

c = 5 

c² = a² + b²

${\mathrm{5²\; =\; 3}}^2+4^2$

25 = 9 +16

25 = 25

LHS = RHS

अतः यह त्रिक पाइथागोरियन प्रमेय को संतुष्ट करता है इसलिए यह ग्रुप (3,4,5) पाइथागोरियन त्रिक है।

पाइथागोरस त्रिगुणों

पाइथागोरस त्रिगुणों की एक अंतहीन सूची है।$जिनमें\; (3,4,5)$पहला पायथागॉरियन त्रिक है। सभी मूल संख्याओं को किसी अन्य धनात्मक पूर्णांक से गुणा करके कुछ और त्रिगुण उत्पन्न किए जा सकते हैं।

n = 3n, 4n, 5n

× 2 = 6,8,10

× 3 = 9,12,15

× 4 = 12,16,20

100 तक की संख्याओं के 16 आदिम पायथागॉरियन त्रिक हैं:

(3, 4, 5)	(5, 12, 13)	(8, 15, 17)	(7,24,25)
(20, 21, 29)	(12, 35, 37)	(9, 40, 41)	(28, 45, 53)
(11, 60, 61)	(16, 63, 65)	(33, 56, 65)	(48, 55, 73)
(13, 84, 85)	(36, 77, 85)	(39, 80, 89)	(65, 72, 97)