Q. Convert the given rational numbers in decimal form:
Q. Find four rational numbers between 7 and 9.
Q. Find three rational numbers between 3/4 and 4/3.
Q. convert the given rational numbers in decimal form:
Q. Expression of Decimal numbers in the form of p/q:
(i) Expression of Decimal numbers 2.45 in the form of p/q
(ii) Expression of Decimal numbers 3.333... in the form of p/q.
Q. Add 2√3 + 4√5 and 3√3 - 7√5
Sol. (2√3 + 4√5) + (3√3 - 7√5)
= (2√3 +3√3) + (-7√5 + 4√5)
= 5√3 - 3√5
Q. Multiply 2√3 by 3√5
Sol. 2√3 × 3√5
= 2 × 3 × √3 ×√5
= 6√15
Q. Divide 8√20 by 2√5
Sol. 8√20 ÷ 2√5
= 8√20 / 2√5
= 4 × √4
= 8
Q. Simplify the following expressions:
(√2 + √3) (√5 - √7)
= √2 (√5 - √7) + √3) (√5 - √7)
= √2 √5 - √2 √7 + √3 √5 - √3 √7
= √10 - √14 + √15 - √21
Task 31: Check your understanding:
Q.1 Add (3√5 + √3) , (-3√5 + 5√3)
Q.2 Subtract (√5 + 7√3) from ( 2√5 - √3)
Q.3 Multiply 3√5 and 5√3
Q.4 Divide 6√10 and 3√2
Q.5 Simplify the following expressions:
(i) (3√5 + √3) (3√5 - √3)
(ii) (3√5 + √2) (√5 - 2√3)
(iii) ( √7 - √3)²
(iv) (√11 + √2) (√11 - 2√2)
(v) ( √2 + 3) ( √2 - 3)
Rationalize
(i) 1/√2
(ii) 1/√5
(iii) ( 1/√3
(iv) (2√11
(v) 3√2/√2
(vi) 2√2/√5
(vii) 6/√3
(viii) 12√2/3√3
Rationalize
(i) (3+√2)/√2
(ii) (3+√2)/(√2+3)
(iii) ( 1/√3
(iv) (2√11
(v) 3√2/√2
(vi) 2√2/√5
(vii) 6/√3
(viii) 12√2/3√3
(3, 4, 5) (5, 12, 13) (6, 8, 10) (7, 24, 25) (8, 15, 17) (9, 40, 41) (11, 60, 61) (12, 35, 37) (13, 84, 85) (15, 112, 113) (16, 63, 65) (17, 144, 145) (20, 21, 29) (28, 45, 53) (33, 56, 65) (48, 55, 73) (36, 77, 85) (39, 80, 89) (65, 72, 97)
पांच सबसे आम पायथागॉरियन त्रिक कौन से हैं
(3,4,5)
(5,12,13)
(7,24,25)
(9,40,41)
(7,24,25)
(9,40,41)
(11,60,61)
पाइथागोरस त्रिक कभी भी सभी विषम संख्याओं या दो सम संख्याओं और एक विषम संख्याओं से नहीं बना होता है
| पायथागॉरियन त्रिगुण | x 2 (समय 2) | x 3 (समय 3) | x 4 (समय 4) |
| 3-4-5 | 6-8-10 | 9-12-15 | 12-16-20 |
| 5-12-13 | 10-24-26 | 15-36-39 | 20-48-52 |
| 7-24-25 | 14-48-50 | 21-72-75 | 28-96-100 |
| 9-40-41 | 18-80-82 | 27-120-123 | 36-160-164 |
| 11-60-61 | 22-120-122 | 33-180-183 | 44-240-244 |

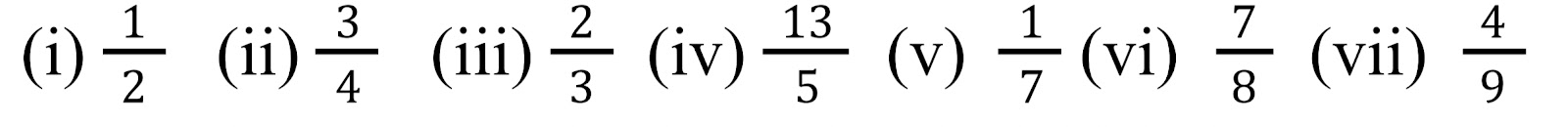



Post a Comment
Post a Comment