Similar Figures
Two figures having the same shape but not necessarily the same size are called similar figures
Two figures having the same shape as well as same size are called congruent figures
Note that all congruent figures are similar but the similar figures need not be congruent.
Similarity of Polygons
Two polygons of the same number of sides are similar if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion)
Similarity of Triangles
Two triangles are similar if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion)
Note : If the corresponding angles of two triangles are equal, then they are known as equiangular triangles.
The ratio of any two corresponding sides in two equiangular triangles is always the same.
Basic Proportionality Theorem (BPT) and its Converse
Basic Proportionality Theorem
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then other two sides are divided in the same ratio. Thus in ∆ABC, if DE || BC, then![]()
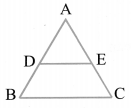
Converse of BPT
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side,
Criteria For Similarity of Triangles
(i) AAA Similarity Criterion : If in two triangles, corresponding angles are equal then their corresponding sides are in the same ratio and hence the two triangles are similar.
(ii) AA Similarity Criterion : If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are similar.
(iii) SSS Similarity Criterion : If in two triangles, corresponding sides are in the same ratio then their corresponding angles are equal and hence the triangles are similar.
(iv) SAS Similarity Criterion : If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportion), then the two triangles are similar.
Areas of Similar Triangles
The ratio of the area of two similar triangles is equal to the ratio of the squares for their corresponding sides thus if ∆ABC – ∆PQR, then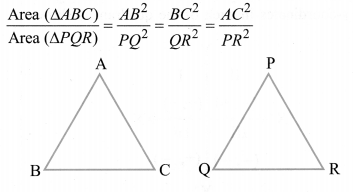
Pythagoras Theorem and its Converse
(i) If perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then the triangles on both sides of the perpendicular are similar to the whole triangle and also to each other.
(ii) Pythagoras Theorem : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Thus in right ∆ABC right angled at B
AC2 = AB2 + BC2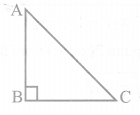
(iii) Converse of Pythagoras Theorem : If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
State and prove Thales Theorem.
or
Prove BPT or Basic Proportionality Theorem.
or
If a line is drawn parallel to one side of a triangle intersecting other two sides, then it divides the two sides in the same ratio.
or
सिद्ध कीजिए कि किसी त्रिभुज की एक भुजा के मध्य बिन्दु से एक अन्य भुजा के समान्तर खींची गई रेखा तीसरा भुजा को समद्विभाजन करती है।




Post a Comment
Post a Comment